Roots of Nonlinear Functions

Roots of Nonlinear Functions - Lab

Section 1

Untar the package of C code on the class website named 'roots.tar'. This will create a subdirectory named 'roots' under the current directory. Change into that 'roots' subdirectory.
In this section we will use two of the root finding algorithms, Newton-Raphson and Bisection, to find the root of the third order polynomial f(x) = x³ - 2x - 5 This polynomial function is discussed in Cheney and Kincaid Computer Problem 3.2.5:

A plot of this polynomial function looks like:

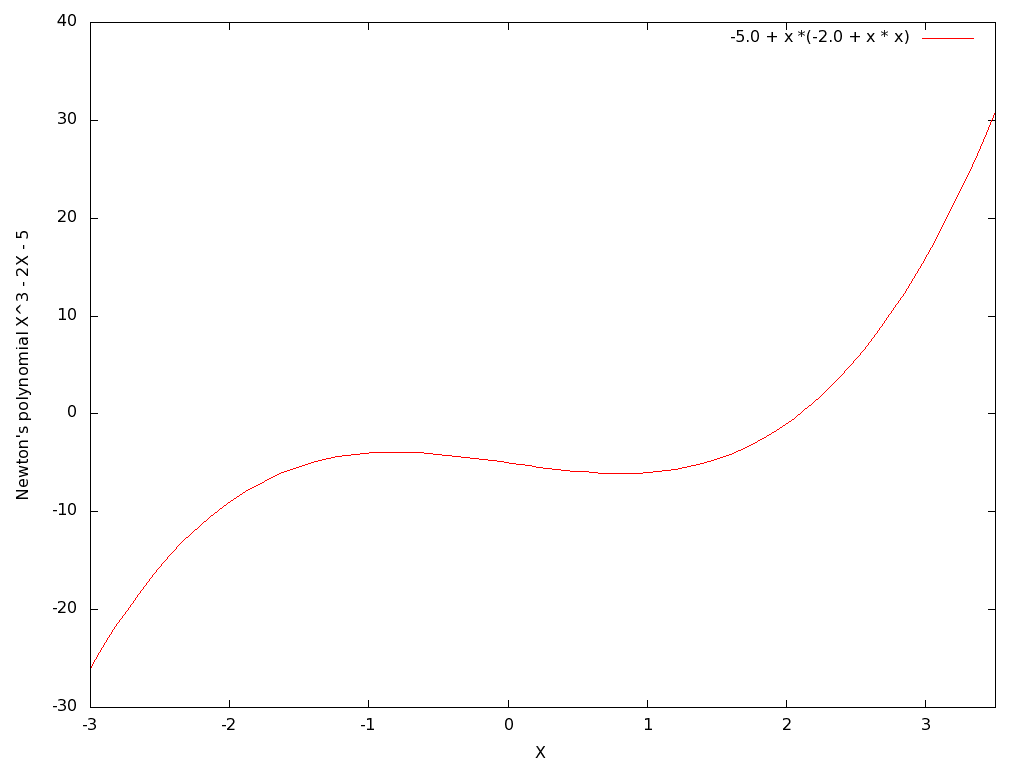
Note that it has a single root at an x value a little greater than 2, and a local minimum and maximum at x = ± sqrt(2/3) ~= ± 0.8164965.

Now in a terminal window, prepare to edit the first C source code file by starting a gedit process running in the background with:

	gedit poly_N-R.c &

Note the ampersand character '&' appended to this command line. This will cause the command to be run in the background but return to a bash shell prompt to allow bash shell commands for compiling and running C code to continue to be run in the terminal. This command starts a gedit process to edit the C source code, and you should see a separate gedit window pop up with the poly_N-R.c source code ready for editing. Read through this short program and see how the main program accepts a command line argument and then calls the function 'newton_raphson', which is supplied by the root finding tools in 'roots.c'. How many maximum iterations are allowed? At what tolerance will the iterations be terminated? The function call to newton_raphson passes two pointers to functions that compute the function to be solved and its derivative. Find those functions at the top of the poly_N-R.c source file and complete the lines indicated with the comments so that the desired polynomial and its derivative will be computed. Use the nested form of polynomial evaluation.

Save your completed source code file and compile it linked together with the roots.c code with the shell command:

	gcc -Wall poly_N-R.c roots.c -o poly_N-R -lm

Now at the shell prompt, run the compiled program and note its help output line:

	./poly_N-R

This is a reminder that the program expects your starting guess for an x value to initialize the algorithm. Since we have seen on the plot above that the root can be expected somewhere in the vicinity of 2, rerun the program giving it a starting guess of 2. How many iterations are required to converge to the root for the given tolerance?

Now explore the behavior of the Newton-Raphson algorithm when the starting guess is not so close to the root. Try starting values of 1 and 3. How does this affect the number of iterations required? Do the polynomial function values at the sequence of trial points always head toward zero in the search for the root?

The Newton-Raphson algorithm is unstable when the starting point, or an intermediate point among its iterations, falls where the first derivative of the function being solved is zero. Now try starting this program with an initial guess of 0.8164965. What happens to the function values at the iteration points? How many iterations are now required for convergence?

Now open the second source code file poly_bisection.c in your gedit window. Copy and paste the corresponding line from your poly_N-R.c source code to complete the function at the top. Note that now the main program collects two arguments from its command line and invokes the 'bisection' function from roots.c to find the root. Compile with:

	gcc -Wall poly_bisection.c roots.c -o poly_bisection -lm

Now at the shell prompt, run the compiled program and note its help output line:

	./poly_bisection

The two arguments expected are of course the two points 'a' and 'b' for the X argument that initially bracket or surround the desired root. Try running this algorithm with a few combinations of bracketing points, for instance, 0 and 4, or -2 and 5, or even a wide range of -10 and 10. How many iterations are required for convergence? What is the behavior of the polynomial function value while the algorithm is iterating? What is the better choice of algorithm for this function?

Section 2

In this section we will use two of the root finding algorithms, Newton-Raphson and Bisection, to find the root of the test function f(x) = sin(x) + x/10 A plot of this test function looks like:

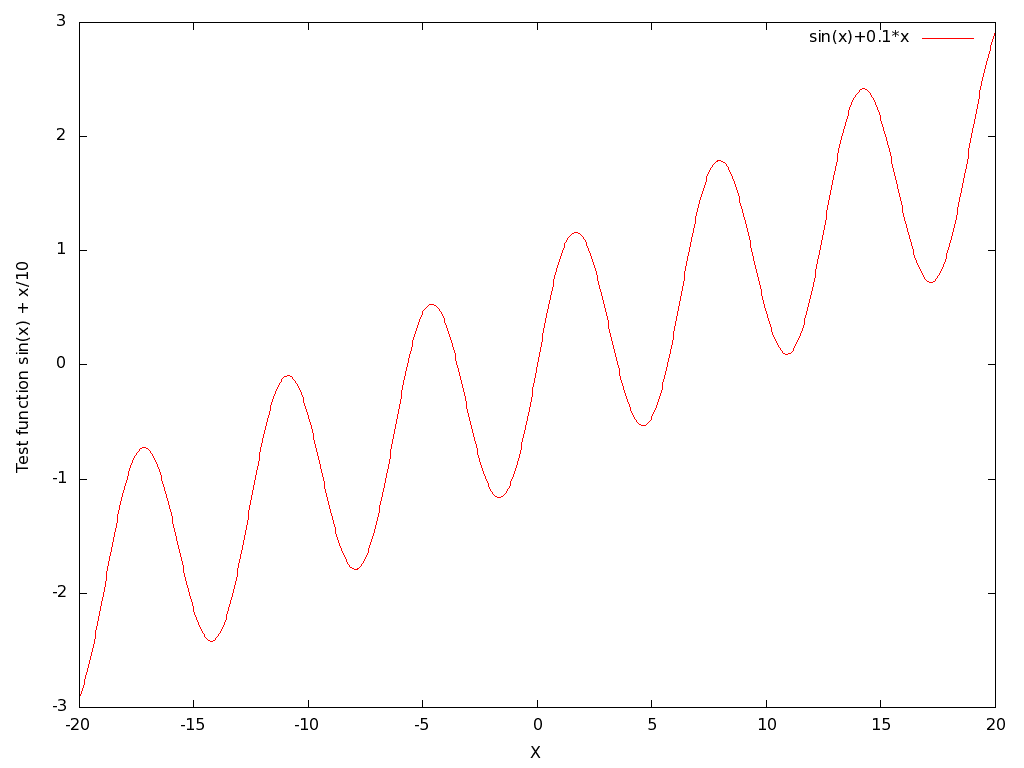
Note that it has a five roots within the range of -20 < x < 20, and various local minima and maxima, two coming relatively close to the X axis.

Now in a terminal window, prepare to edit the first C source code file by starting a gedit process running in the background with:

	gedit sinx_N-R.c &

The function call to sweep_newton_raphson passes two pointers to functions that compute the function to be solved and its derivative. Find those functions at the top of the sinx_N-R.c source file and complete the lines indicated with the comments so that the desired test function and its derivative will be computed.

Save your completed source code file and compile it linked together with the sweep_roots.c code with the shell command:

	gcc -Wall sinx_N-R.c sweep_roots.c -o sinx_N-R -lm

Now at the shell prompt, run the compiled program and note its help output line:

	./sinx_N-R

This is a reminder that the program expects your starting, stopping and increment values for performing an initial sweep through the x values to locate argument values close to a root to use to initialize the Newton-Raphson algorithm. Rerun the program with a sweep specified from -20 to 20 with an increment of 0.1. Are the number and location of the roots what you expect?

Now open the second source code file sinx_bisection.c in your gedit window. Copy and paste the corresponding line from your sinx_N-R.c source code to complete the function at the top. Compile with:

	gcc -Wall sinx_bisection.c sweep_roots.c -o sinx_bisection -lm

Now at the shell prompt, run the compiled program with the same sweep specified as above:

	./sinx_bisection -20 20 0.1