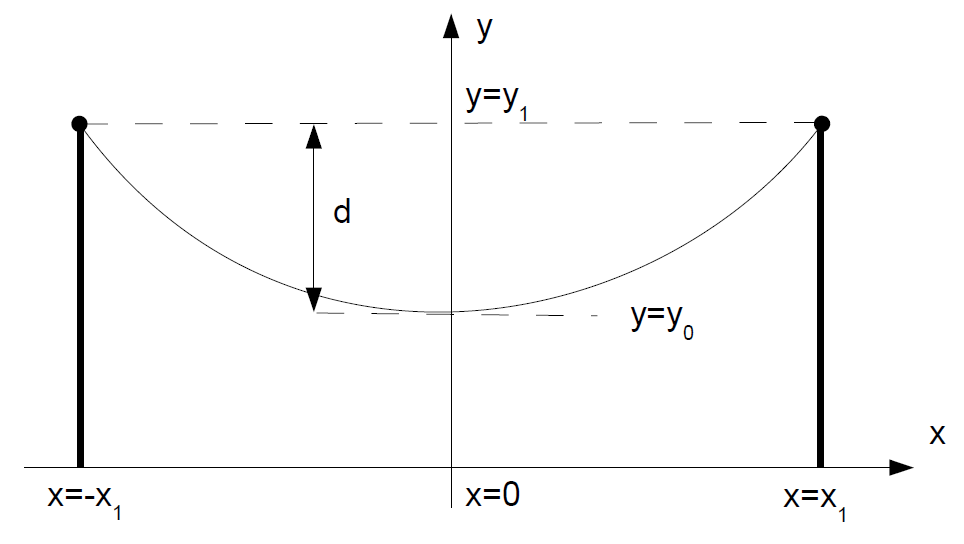
Length=
Consider a perfectly flexible but non-elastic filament with some nonzero mass density. That is, a filament material that can support an infinite tension along its longitudinal direction without deforming, but no tension at all in a transverse direction. Ordinary string or rope or cable approximates this ideal material. Attach two ends of a length of this filament to two supports and let it dangle. What shape is described by the filament when it reaches static equilibrium?

If we assume that the only weight acting on the filament is due to the mass of the filament itself, then a differential equation can be set up to describe the shape of the dangling filament in two dimentions. (See https://en.wikipedia.org/wiki/Catenary for details.) The solution of the shape, called a catenary curve, is
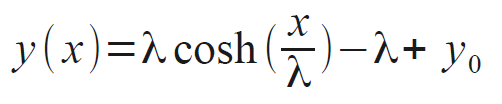
where λ is a parameter, and for the length of the filament is
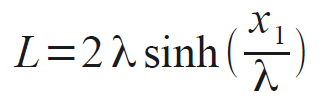
Note that these are transcendental equations in λ, and must be solved numerically.
(Some think that the catenary is also the curve described by the cables of a suspension bridge. While of simular shape, the bridge profile is more closely approximated by a parabola, since the preponderance of the loading on the cable is the weight of the roadway beneath it. This weight is directed uniformly downward, as opposed to the case of the free dangling filament, where the weight is only that of the filament material and thus is along the filament in each differential element.)
The JavaScript application at the top of this page lets you adjust the cable length and see its effect on the cable profile. The solved values of the catenary parameter lambda and the vertical droop distance of the cable profile are displayed. Note that all dimensions are in arbitrary distance units. The x1 coordinate is set to 5 units for this simulation, so the distance between the towers is 10 units.
Back to Computational Physics Playground page
Back to John Fattaruso's home page