This application is an extension of the application that finds allowed energy levels for an electron bound in a single potential well. In this case, however, the potential in which the electron is bound is a double well, that is, two wells separated by some sort of potential barrier.
Solutions of the time-independent Schrödinger equation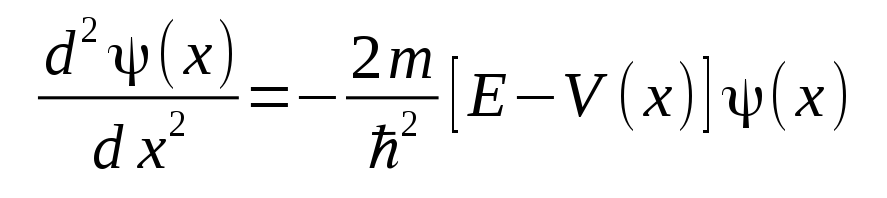
determine the wave function of a bound electron. The potential function V(x) here is assumed to exhibit a central barrier region, and two well regions on either side where the electron energy, E, is higher than the floor of the well, and then also climbs to a field potential that is higher then the electron energy, so that the electron is bound inside either of the two wells. It is a consequence of the wave solutions that there are only certain energy levels that allow the wave solutions to resonate within the structure of the potential wells. In order for it to correspond to a real physical particle, the wave function solution must remain bounded at the extremes of the x coordinate so that the wave is normalizable over all x.
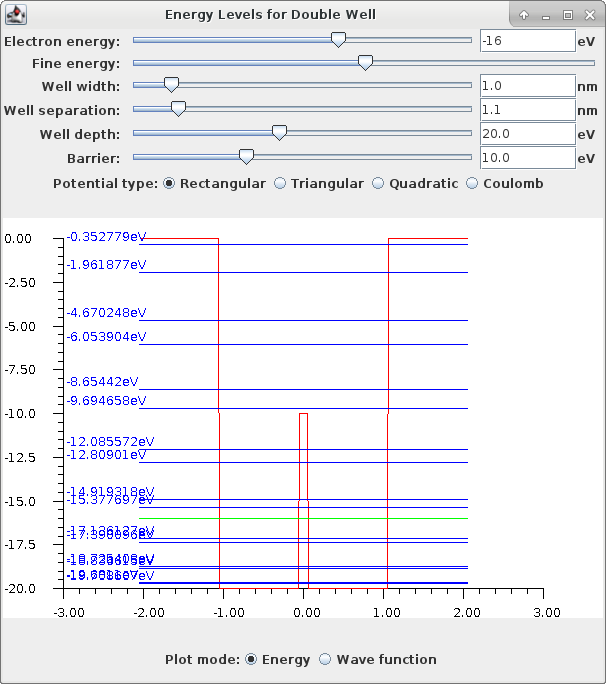
There are two plot modes available, one showing the energy levels, and the other plotting the wave function.
In the wave function mode, the numerical solution of the Schrödinger equation starts at the left hand edge and progresses to the right, as the x value increases. By adjusting the electron energy you can observe that there are only a few values of E that initiate a solution that will end up giving a normalizable wave function at the right hand edge. These energy levels of course correspond with the values with the allowed levels shown in the energy level plot mode. Those allowed levels in blue are solved numerically by the application directly from the Schrödinger equation with a search algorithm that converges automatically on the E values that end up satisfying a condition that indicates the solved wave function is normalizable.
Note that as the separation between the two wells is decreased, for an electron at an energy deep in either well, the lowest allowed energy states are actually split into two levels of very similar energies. This is caused by occasional tunneling exchange of the electron from one well to the other through the central barrier, the liklihood of which is increased as the well separation decreases. The lower of the two split levels will be an even parity solution, symmetric about the center of the central barrier. The higher energy split state is an odd parity solution. The energies of these split states are below and above the energy level allowed when the wells are far apart. The consequence of the existence of the lower even parity solution is the origin of the covalent bond in molecules. As two atoms approach each other, their configuration "falls" down to the lower energy state of closer separation for the symmetrical electron solution. This is equivalent to the atoms experiencing an attractive force, a force which holds them in a covalent bond.
Note: The very lowest energy solutions may not be found for all potential configurations. This is due to the numerical difficulties of searching for a solution over such a wide and varied potential distribution. The search parameters used in this application are a compromise between computation time and search detail.
Run from a shell or command terminal in the download directory with:
java -jar EnergyLevelsDouble.jar
This application lets you find allowed energy levels for an electron in a double potential well. Various profiles of the well potential can be chosen: Rectangular, Triangular, Coulomb and Quadratic. The quadratic profile corresponds to the quantum harmonic oscillator.
Back to Computational Physics Playground page
Back to John Fattaruso's home page