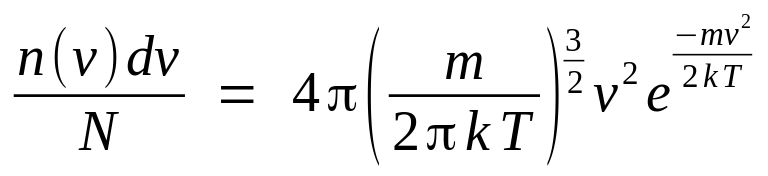
Statistical mechanics has derived the expected distribution of speeds of the molecules in an ideal gas at a given temperature. For a collection of N particles in three-dimensional motion with a constant total kinetic energy, where the particles are free to exchange momentum through elastic collisions, the particle speeds must be distributed following the Maxwell-Boltzman statistics:
where n(v) is the count of particles in a histogram speed bin of width dv centered at speed v. The fraction n(v) / N is the probability per unit bin width of a particle assuming a speed v. We can set up a Monte Carlo simulation of a collection of particles to watch the process of the speed statistics gradually conforming to this theoretical prediction. This simulation can be seen as providing a connection between a statistical, macroscopic view of an ideal gas and the microscopic view of the kinetics of each gas particle.
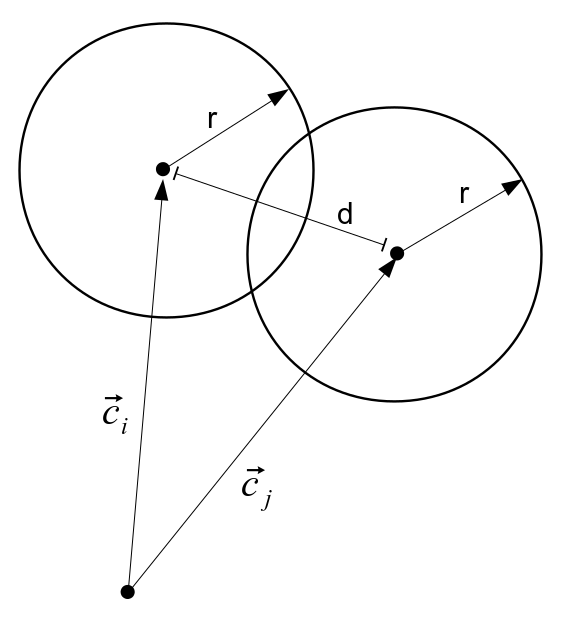
Consider a collection of the N particles freely moving about in three dimensions:
We will keep track of the three dimensional vector of velocity for each of the N particles, but need not track their positions between collisions. In each time step of the simulation we assume that some small randomly selected portion of the particles engage in paired collisions. Since we don't track the path of all the particles between collision events, in order to save a massive amount of computational load, we will simulate a collision between randomly selected pairs of the particle population by simply setting up a number of localized "billiard ball" collisions with a randomly arranged impact parameter. The equations of motion are simulated in a localized coordinate system for each collision by setting up each selected particle pair with initial positions chosen so that the intial particle velocities at the beginning of the time step would carry them to the local coordinate system origin at the same time. The position of one of the particles is given a small random three-dimensional offset, on the order of the particle radius, to simulate the case of the population of particles covering some much larger volume and occasionally engaging in collisions at essentially random trajectories.
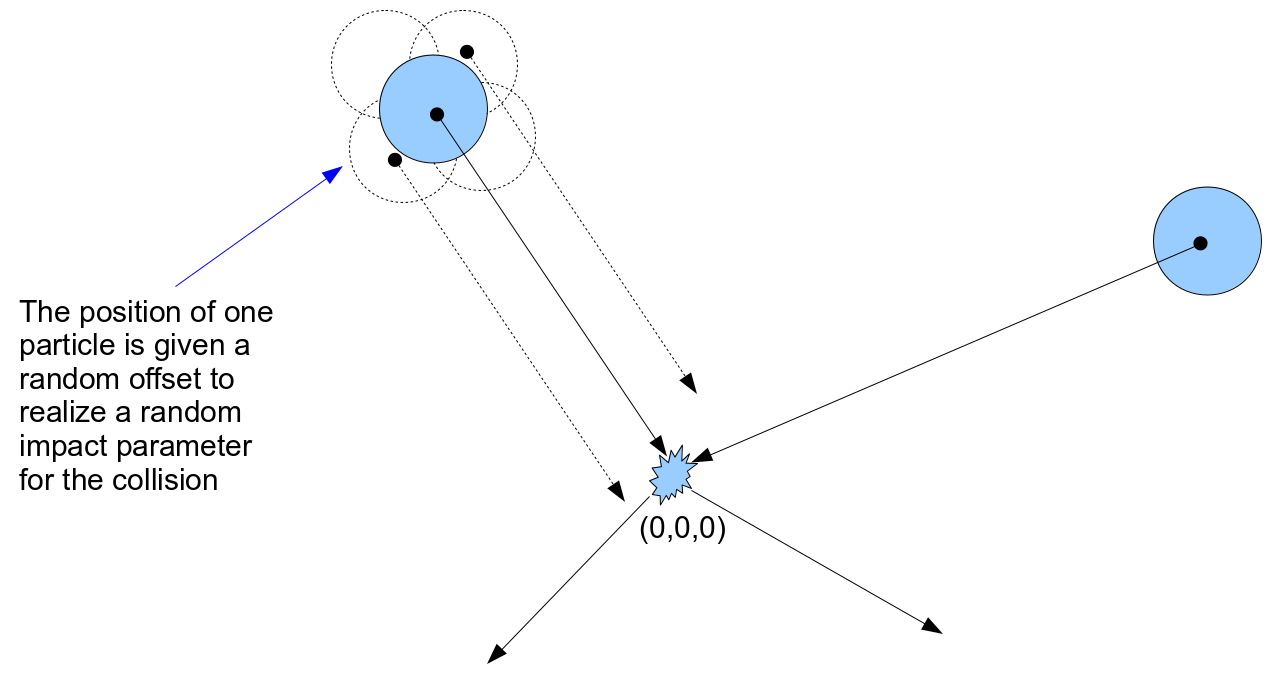
The motion through a collision is simulated with a three dimensional Runge-Kutta solution of the equations of motion. There are assumed to be no forces working on the particles unless their radii overlap, and their motion is free. But an elastic repulsive force is applied to the two particles whenever overlapping radii are found, in proportion to the overlap distance:

where k is a suitably chosen "spring constant". After the collision is simulated, the two final particle velocities are recorded as their new velocities in the particle population.
Pictured here are four example random collisions in three dimensions, where the center vector of each particle in the colliding pair is plotted in the localized collision coordinate system:
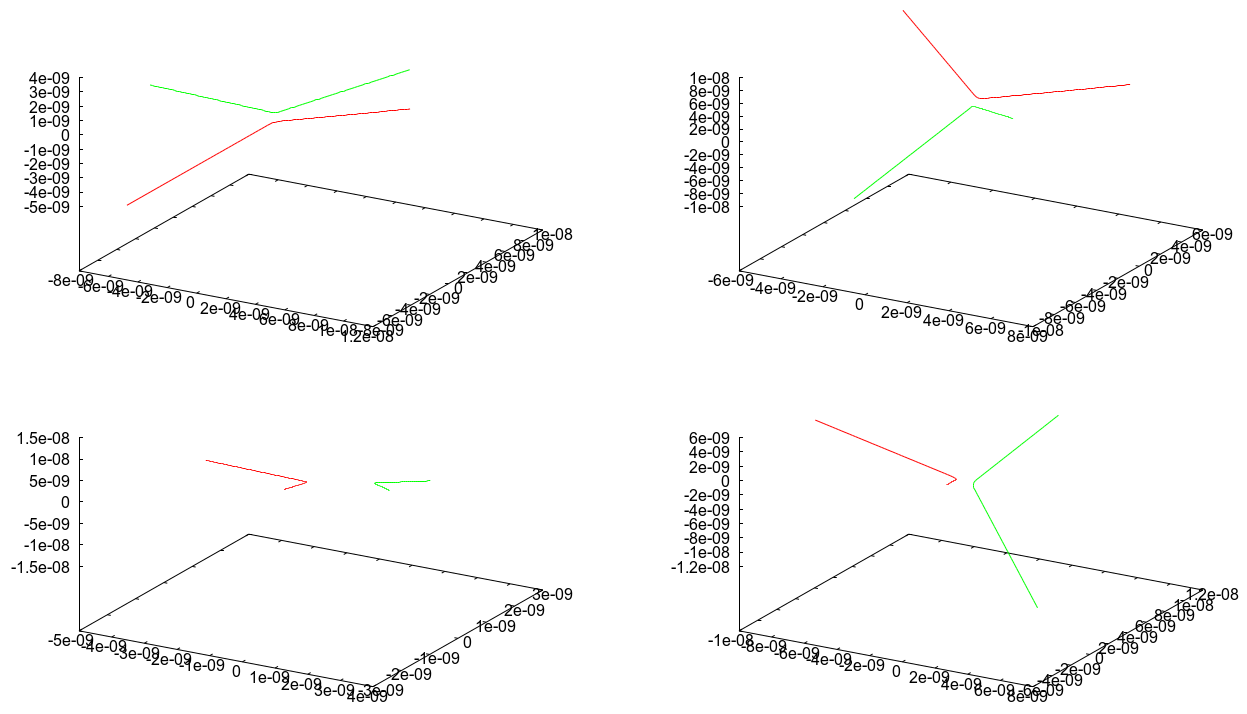
Since we know the theoretical statistical prediction of the distribution of speeds, we can initialize the population of particles with speeds such that their total kinetic energy corresponds to a given temperature. The simulation tool here initializes the population so that every particle has the same identical speed, but at randomly chosen velocity vectors distributed around a three-dimensional direction. The speed is set so that each particle's kinetic energy is 3kT/2, where k is Boltzmann's constant and T is the absolute temperature.
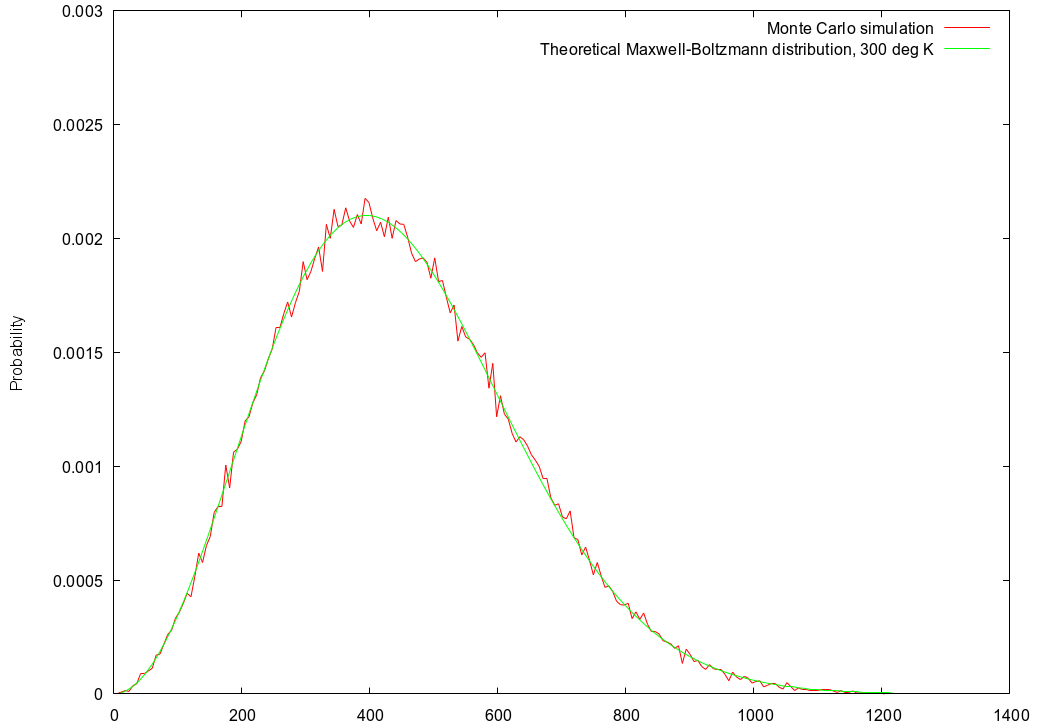
The simulator displays the histogram of particle speeds after each time step. With all particles at one identical speed, the initial histogram displayed will be a tall vertical spike at one velocity. As the simulation proceeds, we can see the spike slowly dissolve and the statistics gradually conform to the predicted Maxwell-Boltzmann distribution, eventually looking like this example for oxygen molecules:
Run from a shell or command terminal in the download directory with:
java -jar IdealGas.jar
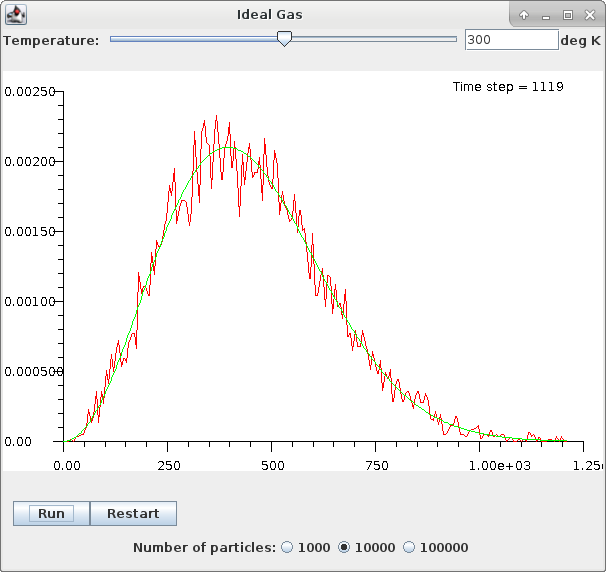
The program allows any absolute temperature to be simulated, and with the population count selected from three possibilities. With a larger population the statistics are smoother, but the simulation proceeds more slowly.
Back to Computational Physics Playground page
Back to John Fattaruso's home page