Watch this nicely made demonstration video on the stability of an inverted pendulum when the pivot point is made to oscillate vertically. That this vertical oscillation will introduce stability to an intrinsically unstable system is a remarkable result. The nonlinear dynamics can be analyzed over only limited ranges with closed form analytic methods, but a more complete picture requires numerical simulation.
The application below is based on a simulation of this geometry:

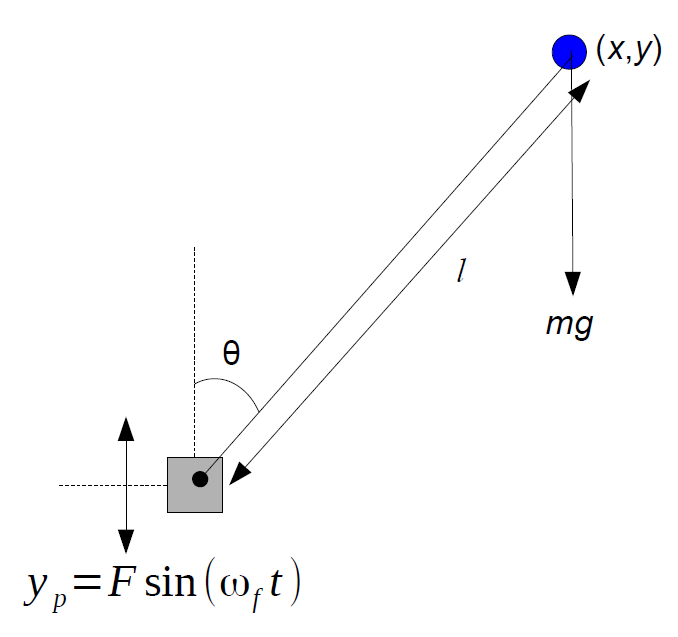
The pendulum comprises a mass m and a rotating arm of length l. The pivot point of the pendulum is mounted on some sort of frame which is made to oscillate with a sinusoidal wave along a vertical axis. The y-coordinate of the pivot point is assumed to be located at y=Fsin(ωft). This dynamic system may be most easily analyzed with Lagrangian mechanics. The Euler-Lagrange equation must be solved with respect to the coordinate θ, the angle between the pendulum arm and vertical. The Lagrangian L = T - V, where T is the kinetic energy and V is the potential energy. For the system pictured above,
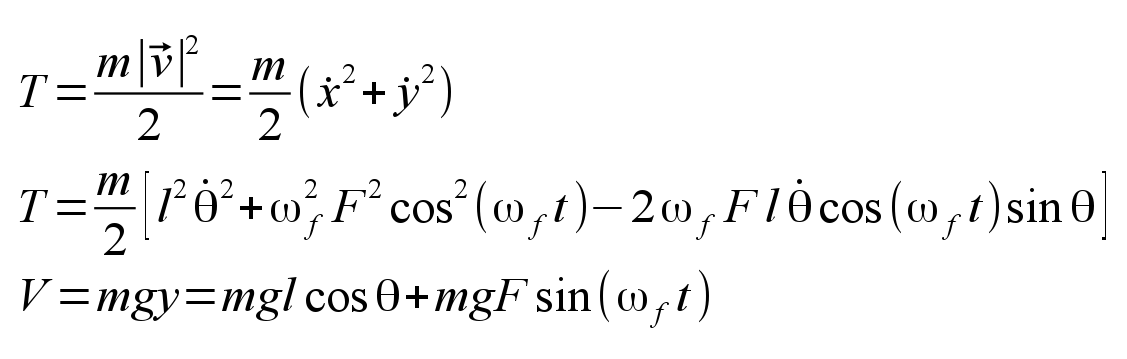
Then the Euler-Lagrange equation gives the second order differential equation of motion:
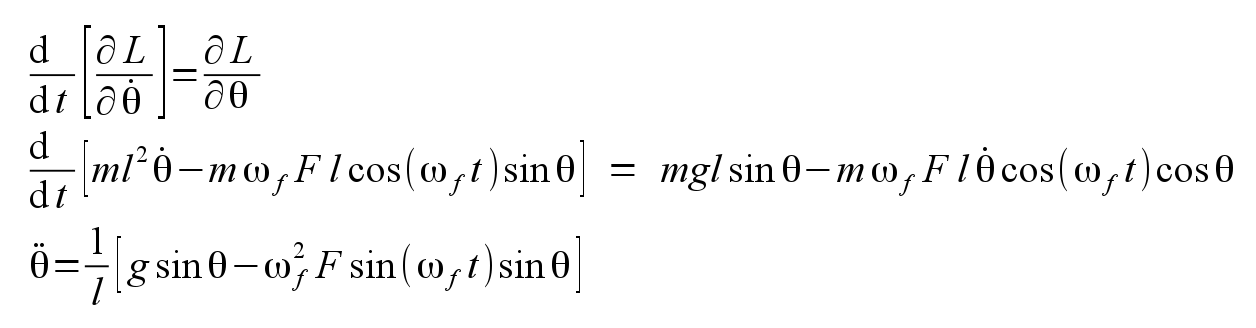
This differential equation can be further put in a form appropriate for numerical solution. This plot shows the expected solution of a 1 meter long pendulum with the forcing coefficient F turned down to zero, or a stationary pivot point:
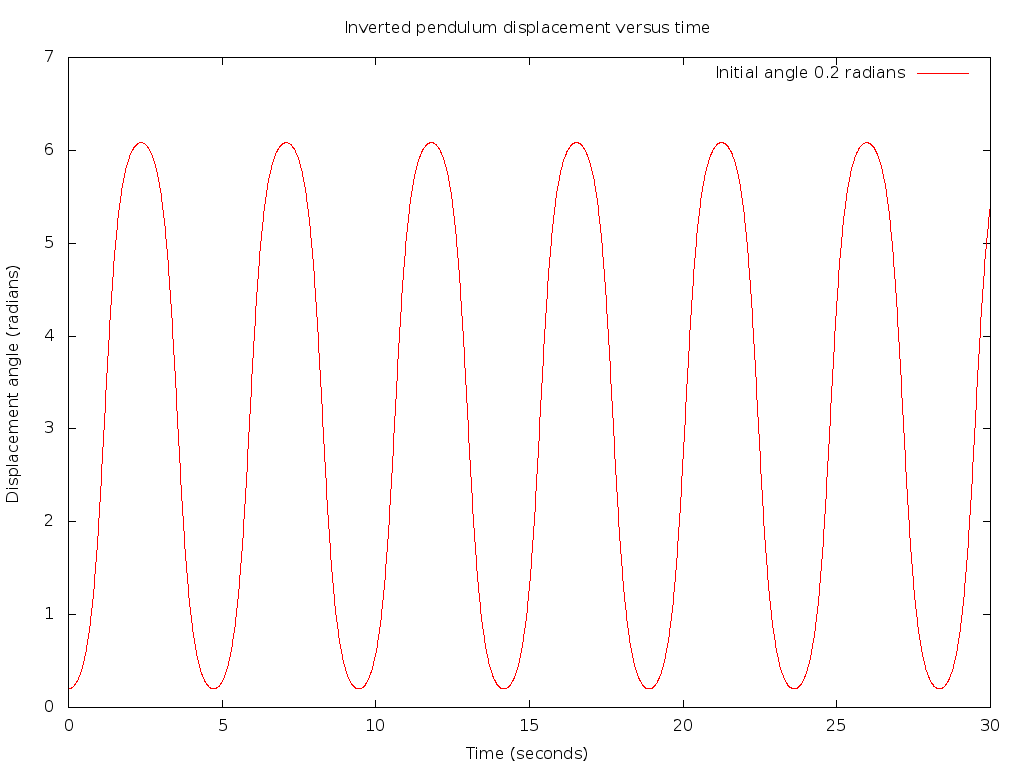
The plot describes the system in the first part of the demonstration video above, before the jigsaw is turned on. The arm angle increases to several radians as the unstable pendulum swings downward, and then with no damping oscillates with the mass below the pivot.
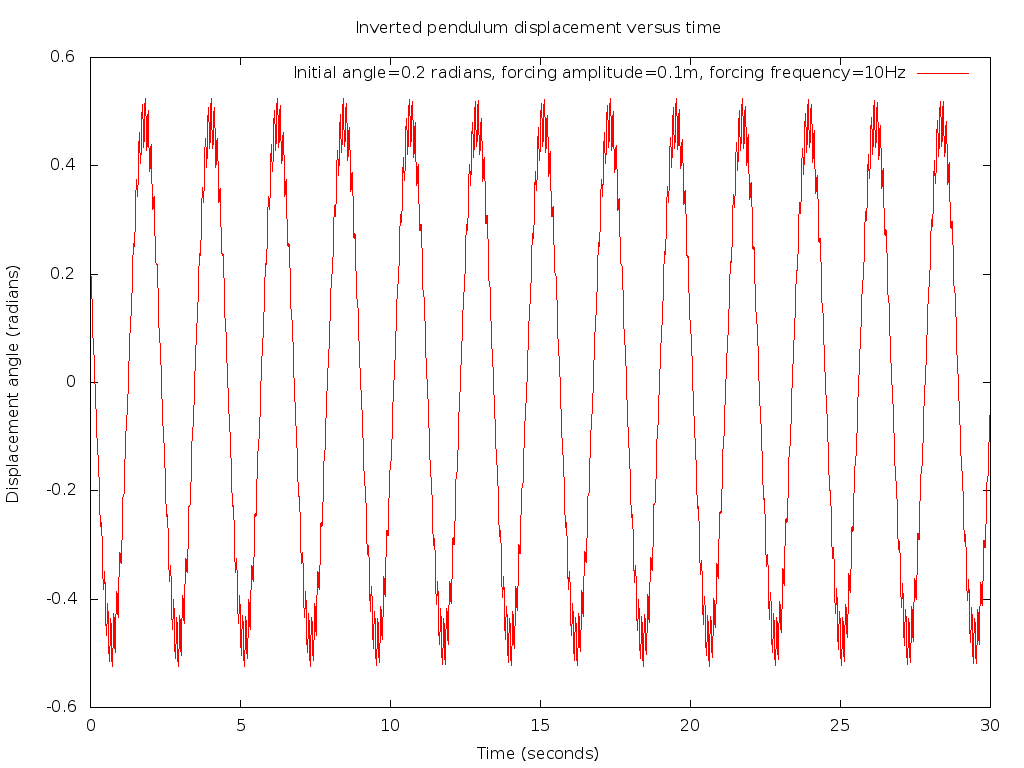
There are many choices of forcing amplitude and frequency of the pivot point that allow the pendulum to stay in a stable inverted orientation, oscillating slowly about a vertical equilibrium with the mass above the pivot. This plot shows the simulation of one choice of forcing, with the frequency ff=10 Hz and the amplitude F=0.1 meters. Note that the displacement angle remains small, indicating a slow oscillation about vertical, similar to the case in the video with the jigsaw running.
Run from a shell or command terminal in the download directory with:
java -jar InvertedPendulum.jar
This application lets you explore the ability to stabilize the inverted pendulum with various adjustments of the pivot forcing parameters. You may adjust the various parameters controlling the simulations by either moving the sliders or by typing in a numerical value and hitting the Enter key.
Back to Computational Physics Playground page
Back to John Fattaruso's home page