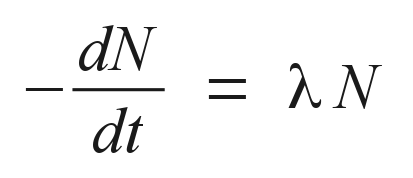
From quantum mechanical principles, we can expect that radioactive species will decay with a constant probability per unit of time. That is, if a sample containing N0 undecayed atoms at an initial time t=0, then the probability of each atom decaying in the next unit of time is λ. Therefore at any time the expected number of atoms decaying in the next unit time interval is λ N(t), where N(t) is the undecayed population as a function of time. A simple first order differential equation may then be written to predict the population of undecayed atoms as a function of time:
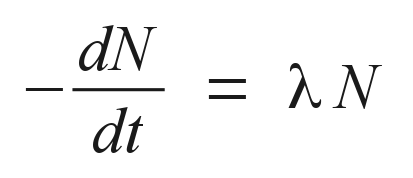
The solution is a straightforward decaying exponential function of time:
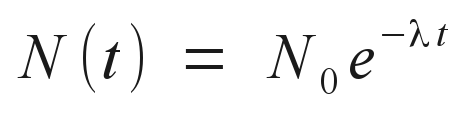
Experimentally, we can measure radioactive decay events by using a Geiger counter or similar instrument, and then we would expect the number of decay events per unit time, or the decay rate, to fall off with the same decaying exponential dependence:
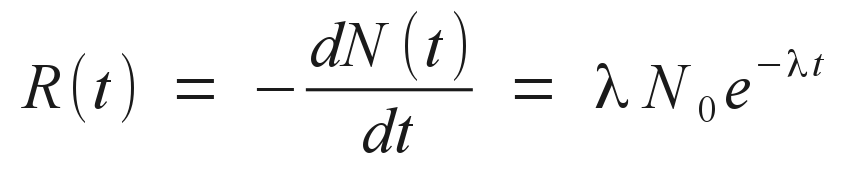
Run from a shell or command terminal in the download directory with:
java -jar RadioactiveDecay.jar
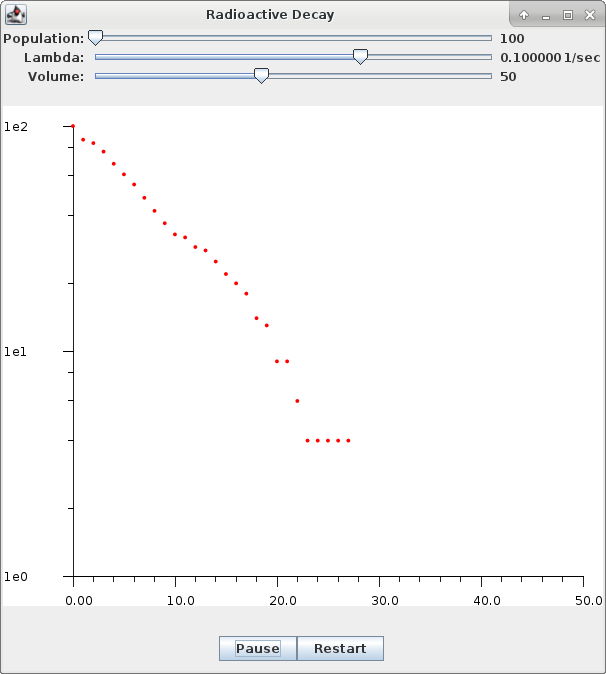
This application simulates the process of radioactive decay with an initial population and a given probability per second λ, by simulating a discrete number of atomic decay events over each one-second time interval. You may adjust the various parameters controlling the simulations by moving the sliders. The plot displays the current undecayed count as a function of time in seconds. Note that the verical population count axis is logarithmic, so a series of populations count readings forming a straight line indicates an exponential decay. If your computer has audio capability, a simulated audio response from a Geiger counter is also provided, with one tick per decay event.
Back to Computational Physics Playground page
Back to John Fattaruso's home page