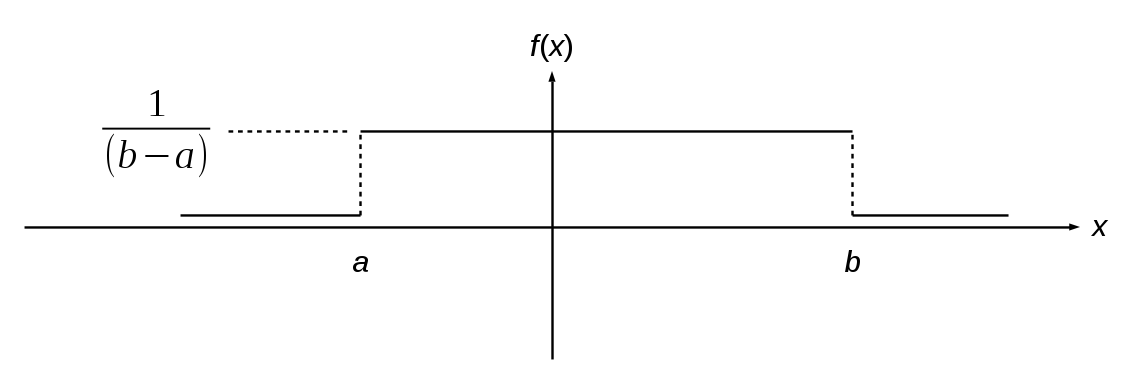
Consider a uniformly distributed random variable with a probability distribution function f(x) shown here:

It is straightforward to derive its mean and variance as:
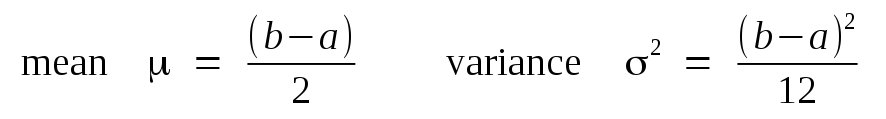
Further, if we form a second random variable by summing N of these uniformly distributed variables together independently, then it is a property of statistical independence that the mean and variance of the sum will be:
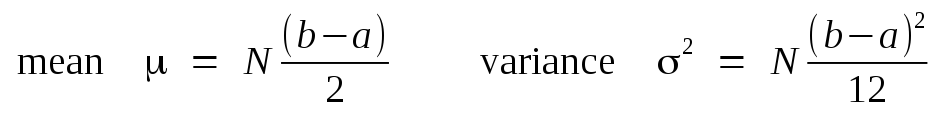
Now suppose we run the following segment of pseudocode:
integer i; real r,x,s1,s2;The two assignment statements to the variables r and x, and then the summation of all the x values into the variables s1 and s2, inside the for loop is simply an example of some numerical computations that may be needed for a numerical analysis algorithm. These particular operations were chosen so that the values of the variable x in successive iterations will be uniformly spread between -0.5 and +0.5. This pseudocode will form in the two sum variables s1 and s2 the sum of N=10,000 such variables. The difference between the two sum variables is that we are subjecting the second variable s2 to a rounding error after only three decimal digits of precision. We will use the example of 10,000 summations here to represent the effects of a long series of numeric calculations that may be necessary for the solution of some quantitative problem. The error that has accumulated in the rounded sum is calculated after the loop has terminated.
To find an experimental estimate of the statistics of this error, the JavaScript code on this web page will run the above segment of pseudocode 500 times in succession, and accumulate the mean and variance of the errors. Click on the 'Replot' button several times to perform many of these experiments and observe the statistics in the plot. You should see the variance of the cumulative rounding error being about 0.0008333 after each set of 500 trials. Why?
We can model the error committed each time a number is rounded to, for example, three decimal places, as the addition of another uniform pseudorandom variable distributed between -0.0005 and +0.0005. This means a variance of 8.3333333×10-8. Over a sum of 10,000 additions of this pseudorandom rounding error, this gives and expected variance of 8.3333333×10-4. Of course, deriving an experimental value for the mean and variance with only 500 trials will exhibit some variation, but these are the typical values observed.
This simple statistical experiment demonstrates that over many thousands of arithmetic operations, typical for a numerical solution to a complex physics problem, considerable numerical rounding error may accumulate. This is why we use the 64-bit double precision floating point numerical format, or even in extreme cases the 80-bit long double format, in practical numerical computation tasks. These formats will introduce rounding errors with a statistical variance so small that even accumulated over many thousands of operations, there is a vanishingly small probability of significant numerical error for most applications.
Back to Computational Physics Playground page
Back to John Fattaruso's home page