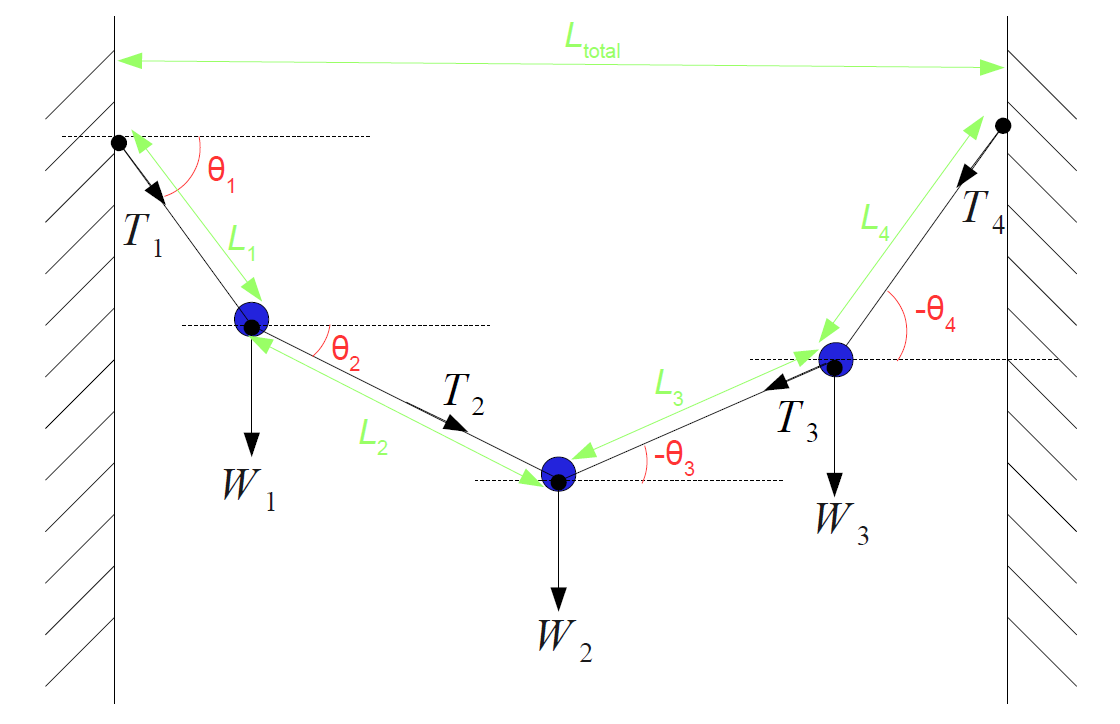
Consider the two-dimensional statics problem pictured here. There are three weights, connected and attached to surrounding walls by four flexible, but massless, strings. The problem is to find the tensions in the strings given the lengths and weights. Note that each angle θi is the angle of each string below a horizontal line.

At first glance, this may appear to be a straightforward statics problem such as commonly solved in elementary Physics courses using systems of linear equations. But a more careful examination will lead one to the requirement of numerical methods. This problem is a fine example of how a deceptively simple physical system admits no analytic solution, and can only be approached by numerical computerized methods.
For similar statics problems to be solved analytically, the angles that the supporting members form with respect to the vertical direction of the gravitational force must be known a priori. This is the case for a fixed structure such as trusses where the elements are composed by rigid materials. But in this problem, the support members are assumed to be flexible strings, and the angles that the strings form when the system reaches a static equilibrium must be solved for in addition to the string tensions.
The basic method for solving statics problems is to find all the components of the forces acting on each weight, and then constrain the sum of all these components to be zero, since by definition in a static equilibrium condition the acceleration on the weights is zero. Resolving the tension in each supporting member involves multiplying the tension that is in a longitudinal direction along a string with either the sine or cosine of the angle formed by the string.
For example, in the figure above, the force on the center weight must balance to zero. The tensions T2 and T3 are shown as acting on the two outer weights, but of course there are identical tensions operating in opposite directions on the center weight. So from the figure, the horizontal components of the forces must balance to zero, and this means that T2cos(θ2)+T3cos(θ3)=0. Similarly the vertical components of the force must also balance to zero, which implies T2sin(θ2)-T3sin(θ3)=W2. Combining similar equations from the other weights gives us a system of equations that must be solved simultaneously.
Now if the angles in a rigid structure are known a priori, the various sine and cosine functions may be evaluated and their values merely form fixed coefficients for the unknown tensions in the system of equations. This leads to a system of linear equations in the unknown tensions that may be solved with straightforward linear algebra tools. However, in this system with flexible strings, the angles themselves are unknown variables to be solved for in addition to the tensions. This implies that the system of equations take the form of transcendental equations, with terms consisting of products of one unknown variable (a tension) with trigonometric functions of other unknown variables (the angles). These types of equations cannot, in general, be solved analytically, and the iterative numerical methods developed by Newton and Raphson must be employed.
Run from a shell or command terminal in the download directory with:
java -jar Strings.jar
This application lets you adjust the values of the weights and string lengths and see the effect these variations have on the solution. The tensions in the four strings are displayed at the bottom of the graphic. These tensions are found in the application code by an iterative algorithm solving the system of nonlinear transcendental equations describing the static condition of this system. Note that the lengths, weights and tensions are expressed in arbitrary units, as tensions will scale linearly with weights, and the lengths are relative to a fixed total length between the walls of 10 units.

Back to Computational Physics Playground page
Back to John Fattaruso's home page