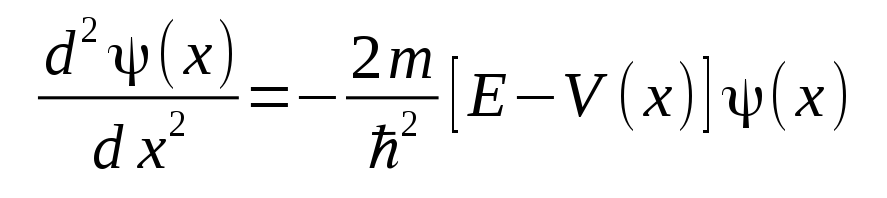
Wave packet a=
Wave packet k0=
Plot mode:
Solutions of the time-independent Schrödinger equation
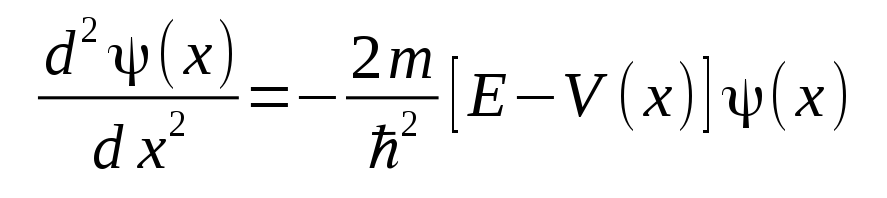
in regions where particles are free to move and not subject to forces, or V(x)=0 and E>0, are of the form
which makes the complete solution including the time dependence
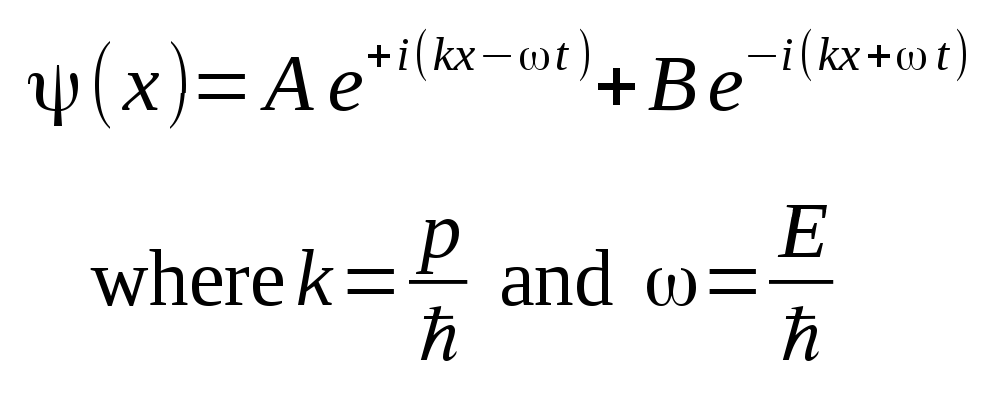
A single wave solution is associated with a continuous flux of particles in the positive or negative x direction, with momentum p and energy E. Solutions that are linear combinations of multiple waves form wave packets that are associated with single particles.
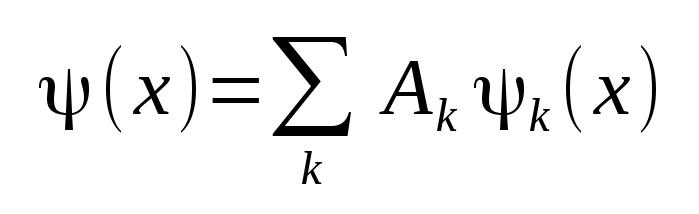
Or in the continuous limit
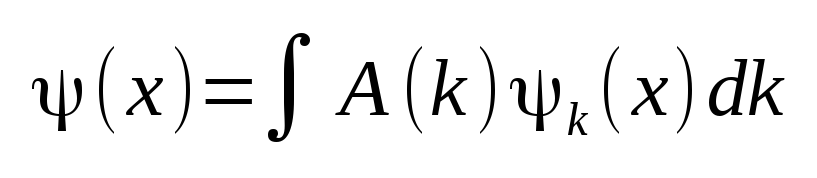
It is mathematically convenient to look at Gaussian wave packets where the weighting factor A(k) that weights the relative contributions of the waves at particular wave number k values in the packet is given by
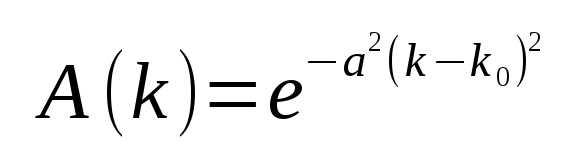
The parameter k0 is the center wave number of the distribution. The parameter a controls the width of the Gaussian distribution in k space around k0, the larger the value of a, the thinner the distribution. This JavaScript simulator constructs wave packets with a discrete number of waves, set at 101, that will be summed and plotted as a function of space and time.
The simulator runs a wave packet propagating in the positive x direction from time zero, and time can be reset to zero at any time by pressing the "Restart" button. You may vary the k0 parameter to adjust the particle momentum and observe the propagation run at different speeds, and vary the a parameter to observe the relationship between uncertainty in momentum and uncertainty in postition. Running the simulation for a long time also allows you to observe the phenomenon of wave packet spreading or dispersion.
There are three plot modes to choose from, the default where you can see both the real and imaginary components of the complex valued wave packet. Also available is a view of the magnitude squared of the wave function, which is of course a measure of the probability distribution in space of the particle. The first plot mode shows the distribution weighting of the discrete wave numbers in k space, directly controlled by the parameters k0 and a.
While the wave packet is propagating during a simulation, statistical computations are also run on the mean and variance of the wave number and position distributions. These computations are displayed across the top of the plot in real time, along with the product of the variances. The Heisenberg Uncertainty Principle states that the product of the variances must be at least 1/4. Watching this computation as the time is advanced allows you to verify this fundamental law of Quantum Mechanics, and quantitatively observe the wave packet spreading.
Back to Computational Physics Playground page
Back to John Fattaruso's home page