The Bohr Model and the Hydrogen Spectrum


SPECIFIC OBJECTIVES

To understand the Bohr model of the hydrogen atom; to determine experimentally the Rydberg constant.

EQUIPMENT

Spectrometer, diffraction grating, hydrogen light source, high-voltage power supply.

BACKGROUND

Early spectroscopists discovered that every chemical element and compound has a unique discrete bright-line spectrum which can be used to distinguish it from all other elements and compounds. This is how we know, for example, the composition of stars without ever having visited one for a sample of material.

In 1885, through a feat of inductive reasoning, Balmer discovered, in a totally empirical way, the formula for calculating the visible wavelengths present in the hydrogen spectrum. That is, Balmer did not derive his formula from a theory like Quantum Mechanics; he simply manipulated the numbers until he found a pattern. A glance at the visible hydrogen wavelengths in the table below will indicate the magnitude of his feat! Subsequently, after much work attempting to explain why Balmer's formula gives the visible hydrogen wavelengths so precisely, in 1913 Bohr provided a mathematical model from which Balmer's formula could be derived. It is interesting to note that 28 years passed between Balmer's formula and the theoretical explanation for it.

At first, Bohr's model was difficult to believe because one feature of the model was so strange: the orbital electron in the hydrogen atom had certain "permitted" orbits in which it would not emit light (even though electric charges moving in circles must emit light according to the classical electromagnetic theory). Bohr's electron would emit light, however, if it "jumped" from one permitted orbit to another permitted orbit of lower energy. (To jump from a low-energy orbit to a higher-energy orbit, the electron must absorb light.)

Balmer's formula is

1 / lambda = R (1 / n12 - 1 / n22 )


where R is called the Rydberg constant with value 109,677.58 cm-1, n1=2 for the Balmer series of wavelengths, and n2 = 3,4,5, ... Each different value of n2 corresponds to a different wavelength (lambda) in the series.

Further Reading

Page 1, Page 2, Page 3, Page 4.

PROCEDURE

Calibrating the Spectrometer

Check to ensure that the spectrometer is still calibrated by aligning the hairline with the stationary side of the slit using the straight through beam. The angle scale should read 0.0o.

Measuring

  1. CAUTION: The difraction grating is a photographic reproduction and should NOT be touched. The deeper recess in the holder is intended to protect it from damage. Therefore, the glass is on the shallow side of the holder and the grating is on the deep side.

  2. Place the grating on the center of the table with its scratches running vertically, and with the base material (glass) facing the light source. In this way, one can study diffraction without the complication of refraction (recall from the previous lab how light behaves when traveling through glass at other than normal incidence). Fix the grating in place using masking tape.

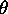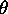  3. Rotate the table to make the grating perpendicular to the incident beam by eye. This is not critical since the average of thetaR and thetaL accommodates a minor misalignment.

  4. Affirm maximum brightness for the straight through beam by adjusting the source-slit alignment. At this step, the slit should be narrow, perhaps a few times wider than the hairline. Search for the spectrum by moving the telescope to one side or the other.

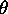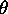  5. For each of the four colors in the hydrogen spectrum, measure the angles thetaR and thetaL to the nearest tenth of a degree by placing the hairline on the stationary side of the slit.

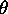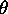    Wavelength (angstroms) Color Intensity thetaR thetaL theta
    6562.8 Red Strong      
    4861.3 Cyan Strong      
    4340.5 Indigo Strong      
    4101.7 Violet Weak      


    Hydrogen Spectrum


Analysis

  1. Average the right and left angles for each color.

  2. Use the grating equation with d = 1 / N to find the wavelength lambda for each color, where "N" is the grating constant determined experimentally in the previous laboratory exercise.

  3. Calculate the percent deviation for each wavelength using
    % deviation = (data-theory)/theory x 100%
    where "theory" is the tabulated wavelength. Do not ignore the sign; it contains information. A positive % deviation means that the value is above the theory; a negative % deviation means that the value is below the theory.

  4. Use your experimental values of lambda and the theoretical value of the Rydberg constant (109,677.58 cm-1) in the Balmer formula to determine n2 for each color. Remember that n2 must be an integer greater than 2. Round your experimental n2 to the nearest integer.

    If all four of your n2 values are very nearly 2, you have performed the unit conversion from angstroms to centimeters incorrectly. Remember that 108 angstrom = 1 cm.

  5. Use your experimental values of lambda and the integer n2 values just found above in the Balmer formula to determine an experimental value of the Rydberg constant for each of the four colors.

  6. Report the best value of the Rydberg as the average of the four values found above.

  7. Report the error on the best value of the Rydberg as the standard deviation of the mean (SDOM). See Taylor section 4.4 if you are confused.

  8. Does your best experimental value of the Rydberg agree or disagree with the theoretical value? See Taylor page 5 if you are confused.



Don't forget your two random and two systematic error sources.



<-- Back to the Electricity and Magnetism Manual