Magnetic Dipole Moment
SPECIFIC OBJECTIVES
To determine the strength of the Earth's magnetic field in Dallas.
To determine the magnetic dipole moment of a magnet.
EQUIPMENT
Helmholtz Coils, multimeter
functioning as an ammeter, DC power supply, ruler, stopwatch, cylindrical
magnet, compass, thread, triple
beam balance, Vernier caliper,
and micrometer.
BACKGROUND
The magnetic dipole moment of a substance (how well it acts as a
magnet) can be determined by suspending a sample of the substance on a
torsion fiber and measuring the period of the oscillations of the
sample in an applied magnetic field. The larger the magnetic dipole
moment, the faster the oscillation.
In this experiment, a permanent magnet in the shape of a thin
cylindrical rod is suspended from a rigid support by a cotton
thread. The cylindrical axis of the magnet is in the horizontal plane,
and thus the plane of oscillation is also the horizontal plane. The
equilibrium direction of the magnet is determined by the horizontal
component of the Earth's magnetic field; that is, the magnet acts as a
compass and aligns itself north-south.
When the magnet is displaced from its equilibrium direction, it
oscillates in simple harmonic motion. The period of the oscillation
depends on the magnetic dipole moment of the magnet and on the
strength of the magnetic field; thus, if an additional magnetic field
is applied the period of oscillation can be changed. By measuring the
period as a function of the applied field and plotting a graph of the
results, one obtains a straight line from which the magnetic moment of
the magnet and the horizontal component of the Earth's magnetic field
can be calculated.
THEORY
The equation of motion of the magnetic torsional oscillator is gven by
I d 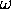 / dt =
NF + NB
where I is the moment of inertia of the rod,
I = M L2 / 12
/ dt =
NF + NB
where I is the moment of inertia of the rod,
I = M L2 / 12
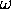 is the angular velocity,
NF is the restoring torque due to the suspension fiber, and
NB is the restoring torque due to the magnetic field.
NB =
is the angular velocity,
NF is the restoring torque due to the suspension fiber, and
NB is the restoring torque due to the magnetic field.
NB = 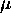 x B
where
x B
where 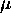 is the
magnetic dipole moment of the magnet and B is the total magnetic field,
that is the vector sum of the Earth's magnetic field BE and
the applied magnetic field BA.
is the
magnetic dipole moment of the magnet and B is the total magnetic field,
that is the vector sum of the Earth's magnetic field BE and
the applied magnetic field BA.
The restoring torque due to the fiber is very small compared to the the
restoring torque due to the magnetic field
NF << NB
so we will neglect NF in the following derivation.
The magnitude of the magnetic torque vector is given by the familiar rule
for the cross product
NB = 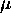 B sin(
B sin( 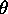 )
where
)
where 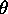 is the angle between
is the angle between
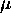 which points along
the cylindrical axis of the magnet and B the magnetic field direction.
which points along
the cylindrical axis of the magnet and B the magnetic field direction.
The angular velocity is the time rate of change of the angle
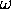 =
d
=
d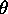 / dt
so the equation of motion can now be written as
I d2
/ dt
so the equation of motion can now be written as
I d2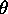 / dt2 =
/ dt2 = 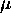 B sin(
B sin( 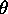 )
This differential equation is non-linear and very difficult to solve so we
will make another approximation (the first approximation was neglecting
NF). For small angle oscillations
(
)
This differential equation is non-linear and very difficult to solve so we
will make another approximation (the first approximation was neglecting
NF). For small angle oscillations
( 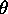 < 20o), we can
replace sin(
< 20o), we can
replace sin( 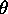 ) by
) by
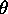 with less than a 2% error.
with less than a 2% error.
The equation of motion is now
I d2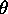 / dt2 =
/ dt2 = 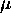 B
B 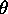 or
d2
or
d2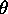 / dt2 = (
/ dt2 = (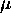 B / I)
B / I) 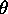 You should recognize this as the equation for simple harmonic motion
with frequency of oscillation given by
2
You should recognize this as the equation for simple harmonic motion
with frequency of oscillation given by
2 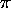 f =
(
f =
(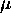 B / I)
½
B / I)
½
If the applied magnetic field is aligned parallel to the Earth's magnetic
field, then
B = BA + BE
In this experiment, the applied magnetic field is created by a pair of
Helmholtz coils. The magnetic field at the center of the two coils is
BA = C i
where i is the current flowing through the wires of the coils, and C is
given by
C = 8 N 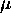 o
/ [(125)½ R]
where N=60 is the number of turns of wire on one coil,
R is the average radius of the
coils, and
o
/ [(125)½ R]
where N=60 is the number of turns of wire on one coil,
R is the average radius of the
coils, and 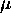 o
= 4
o
= 4 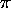 x 10-7 henrys/meter
is the permeability of free space. Be careful! This symbol
x 10-7 henrys/meter
is the permeability of free space. Be careful! This symbol
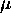 o has an
entirely different meaning than
o has an
entirely different meaning than
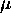 the magnetic dipole
moment -- even the units are different.
the magnetic dipole
moment -- even the units are different.
The equation for the square of the frequency of the magnet's oscillation is
f 2 = (C 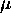 / 4
/ 4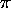 2 I) i +
(BE
2 I) i +
(BE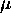 /
4
/
4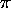 2 I)
Notice that f 2 is a linear function of the current i.
This equation looks like the equation for a straight line
y = m x + b
If f 2 is plotted vs. i, the slope of the resulting straight line
allows a calculation of the magnetic dipole moment
2 I)
Notice that f 2 is a linear function of the current i.
This equation looks like the equation for a straight line
y = m x + b
If f 2 is plotted vs. i, the slope of the resulting straight line
allows a calculation of the magnetic dipole moment
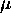 .
Furthermore, once
.
Furthermore, once 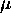 is
determined, the y-intercept allows a calculation of the horizontal component
of the Earth's magnetic field BE.
is
determined, the y-intercept allows a calculation of the horizontal component
of the Earth's magnetic field BE.
PROCEDURE
- Use MKS units throughout this lab. That is, convert all length
measurements to meters, all mass measurements to kilograms, etc.
If MKS units are used for the inputs to calculations, the results will
automatically come out in MKS units as well. The units of magnetic dipole
moment are A.m2 (amp meter2) and the units of magnetic
field are T (tesla).
- Use a ruler to measure the average outer radius of the coils. Each
coil should be measured several times in different directions and the
results for both coils averaged together.
- Next, we need to calculate the inner radius of the coils. This is
where the wood stops and the copper wire begins. The total number of
turns of wire on both coils together is 120. There are N=60 turns on each
coil. Measure the diameter of the copper wire several times using a micrometer under the platform where
the wire is easily accessible. DO NOT PULL THE WIRE OUT OF THE
COILS! Count the number of turns of wire visible in the top layer.
You can now calculate how many layers deep the copper is wound, and
knowing the diameter of the wire you can find the inner radius of the coil.
- Find the average radius (R) of the coils by averaging the inner and
outer radii. Use this average radius to calculate C.
- Use a triple beam balance to
measure the mass (M) and a Vernier
caliper to measure the length (L) of the cylindrical magnet. Record
these data for use in calculating the moment of inertia (I) of the magnet.
- Suspend the magnet by thread so that it hangs in the central region of
the coils. Adjust the thread so that the magnet hangs in a horizontal
level position.
- When the freely suspended magnet becomes stationary, it will point in a
magnetic north-south direction (by definition). Verify this direction
with the compass held far away from the metal tables and coils.
- Connect the coils, power supply, and
ammeter in a series circuit. This
allows the coil current (i) to be read as the supply voltage is varied.
- Supply about 0.30 amps to the coils. Pull the magnet out of the way
while holding the compass between the coils. Note the direction of the
applied magnetic field. Rotate the coils so that the applied magnetic field
aligns with the Earth's magnetic field. Replace the cylindrical magnet
and make sure that it is level.
- Supply 0.20 amps to the coils. Wait about thirty seconds for the coils
to reach thermal equilibrium. Readjust the power supply if necessary.
Set the magnet into oscillation about an axis along the thread with amplitude
no more than about 20o. Time 20 oscillations. Calculate the
frequency (f).
- Repeat for currents 0.30 A, 0.40A, ..., 1.20A.
ANALYSIS
- Plot f2 vs. i and fit the best straight line though the data.
- Find the magnetic dipole moment of the magnet from the slope of the plot.
No error estimate is required.
- Use the magnetic dipole moment of the magnet and the y-intercept of the
plot to calculate the horizontal component of the Earth's magnetic field.
No error estimate is required.
- Find C numerically with units and an error estimate.
- Find I numerically with units and an error estimate.
- Why was it desirable to limit the coil current to 1.2 A? List several
reasons.
- Identify two sources of random error and two sources of systematic error.
- How would your plot differ if the Earth's magnetic field BE
and the applied magnetic field BA had been in opposite
directions rather than in the same direction? (Hint: Would the slope change?
Would the y-intercept change?)
 Back to the Electricity and Magnetism Manual
Back to the Electricity and Magnetism Manual
 Back to the Electricity and Magnetism Manual
Back to the Electricity and Magnetism Manual