Electric Field and Electric Potential

SPECIFIC OBJECTIVES

To determine the shape of equipotential surfaces and electric field lines associated with (a) two point charges (called a dipole when + and -) and (b) two parallel plates, and to compare each of these to theoretical predictions.

EQUIPMENT

Overbeck Electric Field Apparatus with a probe, a two-point board and a parallel-plate board, multimeter used as a galvanometer, 2 sheets of standard paper, power supply, analog voltmeter, hook-up wire.

GLOSSARY

COULOMB'S LAW is that the magnitude of the force (F) that one point charge (q) exerts on another point charge (q') separated by a distance (r) is given by F = kqq' / r² where k is a proportionality constant. The direction of the force is along the line between the two charges. Like signed charges repel and unlike signed charges attract.
The ELECTRIC FIELD (E) at a point is defined to be the Coulomb electric force (F) per unit positive charge (q) at the point E = F / q Note that E is a vector in the direction of the force F on a positive test charge and has units of N/C (newtons per coulomb).
The ELECTRIC LINE OF FORCE is the path a free positive test charge would follow so its direction is generally away from positive charges and towards negative charges. The electric field is tangent to the electric line of force. The strength or intensity of the electric field can be described graphically through the density of electric lines of force: the electric field is strongest where the lines appear closest together.
The ELECTRICAL POTENTIAL difference or VOLTAGE difference (V) between two points is defined to be the work (W) done by the electric force in transporting a unit of positive charge (q) from one point to another. V = W / q Note that electric potential (or voltage) is a scalar quantity and the unit, volt, is defined to be V = J/C (joule per coulomb). Note also that if work is done on the positive test charge being transported, then its potential energy increases and it goes to higher (more positive) electric potential energies.
An EQUIPOTENTIAL SURFACE is a mathematical surface on which a test charge can be moved without any electrical work being done. Since work involves parallel components of force and displacement, it follows that equipotential surfaces and electric lines of force are everywhere at right angles, i.e., the test charge must move perpendicular to E-lines (direction of force) if no work is done.
The ELECTRIC CURRENT (i) is the rate at which charge flows. The unit, ampere, is defined by A = C/s (coulomb per second). The direction of current flow is the direction in which positive charge moves, which is opposite to the direction in which negative charge moves. Since negatively charged electrons carry the current in most materials, it is important to remember that current flows opposite to the way the electrons are moving.
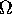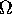The ELECTRICAL RESISTANCE (R) of a device is defined to be the ratio of the voltage (V) across the device to the current (i) through the device R = V / i. The unit of resistance, ohm ( , the Greek letter capital omega), is then defined to be the resistance when one volt exists across and one amp flows through the device, = V/A.
A GALVANOMETER is a very sensitive current detector which can read current passing through it in either direction i.e., a sensitive, unpolarized ammeter. Its usual function is to indicate a zero current circumstance.

BACKGROUND

From the definitions, electric field shapes are envisioned as families of electric lines of force. Since a line is the path followed by a free positive test charge, the shape and direction of a field about an isolated simple charge distri bution is predictable using Coulomb's Law. Consider an electric dipole which consists of a positive and a negative point charge separated by some distance. Imagine that a small, positive lest charge is released near the +q and consider the path it would follow under the two forces acting on it. The test charge is repelled by the +q and atracted to the -q, weakly or strongly depending on the separation distances according to Coulomb's Law. At every point along the line the net force must be tangent to the line in order to move it along that path. In general, the field of a dipole originates from the +q, bows outward and terminates on the -q. Most general physics textbooks provide an accurate representation of the field of a dipole and other point charge configurations.

Predicting the electric fields of continuous charge distributions such as charged wires or plates is more difficult than for point charges. The methods of calculus are generally used for continuous charge distributions and general physics texts usually provide predictions for the more common distributions such as charged parallel plates. Consider two oppositely charged parallel plates whose dimensions (area) are large compared to the separation between the plates. The predicted field bows outward at the ends (called edge effects); however the more important predictions are that, within the central region between the plates, the electric field has a constant magnitude and is directed perpendicular to the plates from the positive to the negative plate. Theoretically predicted diagrams are shown below.

While theoretical predictions of electric fields for simple charge distributions are readily available, their experimental determination can be tedious. One method is to determine the equipotential lines (or surfaces) and then construct the electric lines everywhere at right angles to the equipotentials. If two points are on an equipotential surface, then the electric current between the two points must be zero. (V = Ri, V = 0 and R is not 0, so i = 0) A sensitive, null detecting ammeter, called a galvanometer, may be used to locate points on equipotentials.

PROCEDURE

Using the two screws provided, install the two-point charge plate on the underside of the board so that the black side is down or away from the board.
Use masking tape to secure an 8.5" x 11" page of paper to the top of the board. The four legs are spring loaded and the corners of the page can fit under them. Use any method to locate the two point charges and mark them on your paper.
Turn the power supply off and the voltage control fully counter-clockwise to zero before connecting it to 110V. AC. Connect the 0-10 DCV meter across the power supply with correct polarities. (+ to + or red-to-red) to use as a voltage monitor.
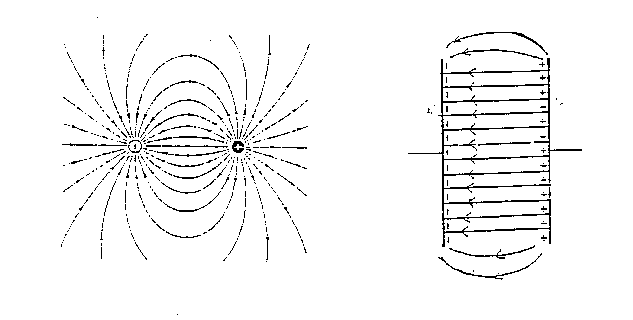
Connect the power supply across terminals A and B observing that A is negative and B is positive as shown in the diagram below.
Read the precautions for using a multimeter as a current meter.
Set the multimeter, which is to function as the galvanometer (G), on the smallest current range and DCA (direct current amps) function. Connect G between terminal E4 and the probe.
Separate the probe enough to fit it over the board with the metal contact touching the black surface and the small hole on the probe above the paper. The board is now ready for use and should be connected as represented in the diagram above.
Turn the power supply on and adjust it to about 8.0 V. (The exact voltage used is not critical because this would not affect the shape of the field even though it does affect the strength of the field.)
With moderate pressure between the probe contact and the black surface of the plate, move the probe to various points between A and B until a point is found where G reads zero and mark this point through the hole in the top of the probe . Finding this null point may be tedious because G is very sensitive and slight variations such as probe pressure may cause it to fluctuate. If it fluctuates between + and - (zero is surely somewhere in between!), this probably is an adequate "zero" reading. Practice finding the null points until a satisfactory technique has been achieved. Realize that each null point found is at the same potential (voltage) as is E4 because no current flows from E4 to the point (P). Thus, all null points found while G is connected to E4 are at the same potential and, therefore, form an equipotential line.
With G connected to E4, find a series of null points and mark each with a pencil through the hole in the top of the probe. There should be enough (8-10) points to allow sketching a smooth curve between them and they should extend from near the top to near the bottom of the page. They need not extend to the left or right beyond the area between A and B. Sketch the smooth curve connecting the null points freehand; do not use a ruler.
Repeat the previous step using other E-points instead of E4 to locate points on other equipotentials. Continue this repetition until equipotential lines for E3, E2, E1, and E5, E6, E7 have been found. (Don't expect perfection in these equipolential curves because the field is likely to be somewhat distorted by the metal parts of the plate and the metal under the table. A conducting material such as most metals, must be considered an equipotential surface so, if E-lines terminate on the surface of a conductor, they must do so at right angles to the surface. Thus, any metal in the immediate vicinity of an E-field could distort the field noticeably.)
Replace the page of paper with a clean sheet and mark the location of the parallel plates on it. Replace the two-point charges plate with the plate having the parallel plate configuration on it. Repeat the two previous steps for the parallel plates.

ANALYSIS

The two pages, one for point charges and one for parallel plates, constitute the raw data. Each partner should analyze both pages and keep one in each lab notebook. By freehand, draw smooth curves through each of the equipotential sets of points found. Sketch in the electric lines so that they are everywhere at right angles to the equipotential lines. Label the polarity of the charges and plates and assign directions (arrows) to all E lines for both pages. The two electric field configurations thus obtained should provide the basis for conclusions to be reached. Partners should each make notes in their individual notebooks that could be used in writing a formal report.

Each partner must answer the following questions in his or her own notebook.

In what general region or regions is the point-charge field strongest? How do you explain this observation? How, if at all, is this related to line density?
In terms of the equipment used, what is the principal explanation or reason for anomalies (deviations from theory) found in the two fields?
Identify at least two sources of random (statistical) error.
Identify at least two sources of systematic error.

CONCLUSION

Summarize what you learned today (not what you did).

Back to the Electricity and Magnetism Manual