Ohm's Law
SPECIFIC OBJECTIVES
- To test Ohm's Law (V = Ri) by plotting V vs. i for a wire and to
determine the resistance (R) of the wire .
- To test the resistivity
law (R =
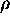 L / A) by plotting R vs. L for a wire and to determine the
resistivity (
L / A) by plotting R vs. L for a wire and to determine the
resistivity (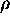 )
for the material of which the wire is made.
)
for the material of which the wire is made.
- To become familiar with the voltmeter-ammeter method for measuring
resistance.
EQUIPMENT
Board with ten 1-meter lengths of a wire mounted between binding posts,
power supply, analog voltmeter,
multimeter used as ammeter and
later as an ohmmeter, hook-up wire,
micrometer.
GLOSSARY
- The ELECTRICAL RESISTANCE (R) of a device is defined to be the
ratio of the voltage (V) across the device to the current (i) through the
device R = V / i. The unit of resistance, ohm
(
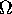 , the Greek
letter capital omega), is then defined to be the resistance when one volt
exists across and one amp flows through the device,
, the Greek
letter capital omega), is then defined to be the resistance when one volt
exists across and one amp flows through the device,
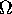 = V/A.
= V/A.
- OHM'S LAW a condition of some materials where the resistance is
constant regardless of the voltage applied across the device. For materials
that obey Ohm's Law (some do not), a plot of voltage vs. current yields a
straight line whose slope is the resistance of the material.
BACKGROUND
For some materials, the resistance is constant no matter how much voltage is
applied across it. These materials are said to obey Ohm's Law. Since the
resistance (R) is constant, a plot of voltage (V) vs. current (i) yields a
straight line for these materials. Notice that resistance is always the
ratio of voltage across a device to the current through the device. But the
resistance is constant only for those materials that obey Ohm's Law. For
this experiment, we will be studying a material known to obey Ohm's Law.
Ohm's Law suggests a method for measurement of resistance. If a voltmeter is
used to measure the voltage (V) across an unknown resistance (R),
and an ammeter is used to measure the current
(i) through the same unknown resistance, then R would be given by R = V/i. The
two measures of V and i should, of course, be made simultaneously. Some
further consideration of the voltmeter-ammeter method (V-A method) reveals
that there is inherent error involved. Consider the two circuits (cct.) shown
below.
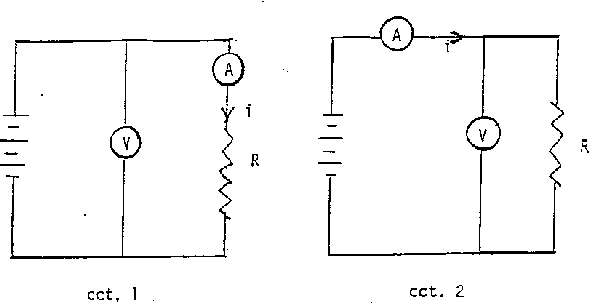 In cct. 1, the ammeter (A) reads the true current (i) through the unknown
resistance (R) but, the voltmeter (V) reads the voltage across both A and
R. Thus, the V-reading is larger than that which is required so the
calculated R would be in error i.e., too large:
Rcalc = (VR + VA) / i
Ammeters are generally
designed to have a small internal resistance (20 ohms) so, if R is large,
then the error (Rcalc - R)
would be small i.e., practically all of the V-measure is across R, and
VA can be neglected compared to VR.
In cct. 1, the ammeter (A) reads the true current (i) through the unknown
resistance (R) but, the voltmeter (V) reads the voltage across both A and
R. Thus, the V-reading is larger than that which is required so the
calculated R would be in error i.e., too large:
Rcalc = (VR + VA) / i
Ammeters are generally
designed to have a small internal resistance (20 ohms) so, if R is large,
then the error (Rcalc - R)
would be small i.e., practically all of the V-measure is across R, and
VA can be neglected compared to VR.
In cct. 2, the voltmeter reads the true voltage across R but now the ammeter
reads the current (i) through both the voltmeter and R. Thus, the measured
current is larger than that which is required so the calculated R
would be in error, i.e., too small:
Rcalc = V / (iR + iV)
Voltmeters are generally
designed to have a large internal resistance (megaohms) so, for practical
purposes, nearly all of the i-measure flows through R, very little current
flows through the high-resistance voltmeter, and
iV can be neglected compared to iR.
Considering the role of internal meter
resistance, cct. 1 is better (smaller error) if R is large whereas, cct. 2 is
preferable if R is small.
The Ohmmeter and Wheatstone Bridge provide two other methods for the
determination of resistance. The ohmmeter is not generally a precision device
but is adequate in many electronic applications. The Wheatstone Bridge can
be refined to provide precision resistance measures as might be required in
the use of such as a resistance thermometer.
A property of electrical resistance which may need to be considered in some
cases is that it depends on temperature to some extent. The resistance (R)
is given by:
R = Ro(1 + 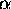 T),
where T is the temperature, Ro is the resistance at
0oC and
T),
where T is the temperature, Ro is the resistance at
0oC and 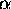 is the TEMPERATURE COEFFICIENT OF RESISTANCE. Fortunately,
is the TEMPERATURE COEFFICIENT OF RESISTANCE. Fortunately,
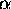 is small for some metals such as copper and aluminum but can be relatively
large for others. The latter are useful as resistance thermometers.
Recalling that the time rate of heat production (Power = P) in a resistance
(R), carrying a current (i) is given by
is small for some metals such as copper and aluminum but can be relatively
large for others. The latter are useful as resistance thermometers.
Recalling that the time rate of heat production (Power = P) in a resistance
(R), carrying a current (i) is given by
P = R i2.
the temperature dependency of resistance may or may not be especially
relevant depending on whether i is large or small.
Ohmic materials or devices are those which obey Ohm's Law but there are
non-ohmic things to which the law cannot be properly applied. While Ohm's
Law does have wide applicability, it does also have limitations.
The RESISTIVITY LAW is that R =
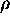 L / A where R is the resistance of a wire of
length L, cross-sectional area A and made of a material whose RESISTIVITY is
L / A where R is the resistance of a wire of
length L, cross-sectional area A and made of a material whose RESISTIVITY is
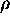 .
Logically, R is proportional to L, and R is also proportional to l/A so
.
Logically, R is proportional to L, and R is also proportional to l/A so
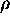 is a proportionality constant which
depends only on the material of which the wire is made and not on the
wire's length, cross-sectional area, or shape.
is a proportionality constant which
depends only on the material of which the wire is made and not on the
wire's length, cross-sectional area, or shape.
One test of the resistivity law could be to measure the resistance (R)
of various lengths (L) of a certain gauge (diameter or cross-sectional
area) and kind (material) of wire. A linear plot of R vs. L should
reveal that R is prportional to L and, according to the law, the slope
of this plot should be
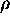 / A.
If the diameter of the wire is measured, from which the area (A) of
the wire may be calculated, then from the slope of R vs. L,
/ A.
If the diameter of the wire is measured, from which the area (A) of
the wire may be calculated, then from the slope of R vs. L,
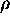 could be found.
could be found.
PROCEDURE
- Read the precautions for using a
multimeter as a current meter. Bear in mind that the colors of the lead
wires in this experiment will differ from the colors of the probes in the
precautions.
- Adjust the power supply to zero volts and connect the circuit as shown
below leaving the voltmeter probe (P) disconnected at this time.

Ohm's Law
- Connect the voltmeter probe (P) to terminal 10 and check the wiring to
see that the voltmeter (V) will read the voltage across the entire 10-meter
length of wire while the ammeter (A) reads the current through the wire. Set
the ammeter on DCA function and on the 10 A range. Set the voltmeter on
DCV function and use the 15V range. Turn the power supply on and slowly
increase the voltage until A and V begin to show readings. It is now a matter
of reading A and V simultaneously to provide data for the V vs. i plot. The
range for i should be from about 0.2 A to about 0.8 A and i should not
exceed 1.0 A. Give some thought to the criteria involved and choose the
current increments to provide an appropriate number and distribution of
points. Record this V vs. i data. In attempting to read voltage and current
simultaneously, perhaps two partners could each read a meter on some signal.
Resistivity Law
- Adjust the power supply to zero volts and remove the probe from the
terminals. Increase the power supply voltage until the current through the
wire is about 0.75 A. After a few minutes, when thermal equilibrium is
reached, the current should stabilize. Touch the probe to the lm terminal and
read and record voltage and current simultaneously. Continue this
procedure until the 2m, 3m...10m. terminals are used recording L, V, and i
at each step.
- Use a Vernier micrometer
to measure the diameter of the wire in several places. Do not stretch the
wire in measuring the diameter. Two measurements on each side-wire should be
adequate. Also, close the micrometer, read it, and make a zero correction on
subsequent readings. A reliable average diameter is needed to ensure that
the calculated area is representative of the wire.
Ohmmeter Method
- Read the precautions for using a
multimeter as an ohmmeter. Bear in mind that the colors of the lead
wires in this experiment will differ from the colors of the probes in the
precautions.
- Use the ohmmeter function of a multimeter to measure the resistance of
the 10-m length of wire. To avoid possible damage to the meter, the
wire must not be connected to the power supply when the ohmmeter is used.
- Short out (touch together) the ohmmeter lead wires to read and record
the lead-wire resistance.
ANALYSIS
Ohm's Law
- Plot V vs. i, read R from the slope, and calculate
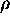
Resistivity Law
- Calculate the propagated error on R from the reading errors on V and i
for each line in your data table.
- Plot R vs. L, read
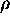 (not equal to the slope, but related simply to it), and calculate R.
(not equal to the slope, but related simply to it), and calculate R.
Ohmmeter Method
- How does the ohmmeter value of R compare to the resistance of 10 m of the
wire as found from your plot of V vs. i? Also, compare to that found
from R vs. L. (Show how you found these latter
R's). Note that this comparison involves the ohmmeter method vs. the
V-A method. Does it seem that the previous ohmmeter reading
should or should not be corrected for the lead-wire resistance? Explain.
In other words, the ohmmeter method gives the resistance of both the board
AND the lead wires; do the other methods measure the resistance of just the
board, or do they also measure the lead wire resistance. If all three methods
measure the same thing, no correction is nesscessary.
- There are now available three different measures (two plots and
ohmmeter) of the resistance of 10 m of the wire. List these three R-values
and calculate the mean and standard deviation on the mean (SDOM).
Now what do you
believe the resistance of your 10-m length to be, in the form of R
±
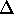 R?
(The point is, that after all this measuring,
R10 is still not exactly known! So - it must be acknowledged
that some measurement error exists in all experimental work.)
R?
(The point is, that after all this measuring,
R10 is still not exactly known! So - it must be acknowledged
that some measurement error exists in all experimental work.)
- Identify at least two sources of random (statistical) error.
- Identify at least two sources of systematic error.
- Bonus: Look up the resistivity of the wire in the CRC Handbook of
Chemistry and Physics and identify the material.
CONCLUSION
Summarize what you learned today (not what you did).
 Back to the Electricity and Magnetism Manual
Back to the Electricity and Magnetism Manual

T),
where T is the temperature, Ro is the resistance at
0oC and
is the TEMPERATURE COEFFICIENT OF RESISTANCE. Fortunately,
is small for some metals such as copper and aluminum but can be relatively
large for others. The latter are useful as resistance thermometers.
Recalling that the time rate of heat production (Power = P) in a resistance
(R), carrying a current (i) is given by
L / A where R is the resistance of a wire of
length L, cross-sectional area A and made of a material whose RESISTIVITY is
.
Logically, R is proportional to L, and R is also proportional to l/A so
is a proportionality constant which
depends only on the material of which the wire is made and not on the
wire's length, cross-sectional area, or shape.
/ A.
If the diameter of the wire is measured, from which the area (A) of
the wire may be calculated, then from the slope of R vs. L,
could be found.

 Back to the Electricity and Magnetism Manual
Back to the Electricity and Magnetism Manual