Archimedes' Principle

Background Reading

Science historians generally agree that the idea for his principle occurred to Archimedes as he entered a bath pool. As he waded into deeper water, the force on his feet became less.

Archimedes' Principle is that an object totally or partially immersed in a fluid (liquid or gas) is buoyed (lifted) up by a force equal to the weight of the fluid that is displaced.

It has numerous applications, one of which is the determination of density and specific gravity. In the following discussion, the subscripts S, W, and A represent the Substance, Water, and Air, respectively.

Density is the mass per unit volume of a substance. 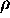= M / V

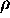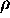Specific Gravity is the ratio of the density of the substance to the density of water. SG = _S / _W.

The metric system unit GRAM is defined to be the mass of one cubic centimeter (one milliliter) of pure water at 3.98^oC. Thus, for water 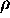_W = 1 gram/cm³ and, if errors due to impurities and/or temperatures are tolerable, this is a great convenience. The definitions given above suggest various methods for determining specific gravity.

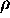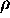SG = _S / _W = (M_S / V_S) / (M_W / V_W) = (M_Sg / V_S) / (M_Wg / V_W) = (W_S / V_S) / (W_W / V_W)

The definition of SG was applied for the first equality; the definition of density was applied for the second equality. For the third equality, the numerator and denominator were multiplied by "g". W_S is the weight of the substance measured in air; W_W is the weight of the water displaced by the substance when it is immersed.

In some circumstances, the volume of the substance is equal to the volume of the water. In particular, when a solid object is completely immersed in water, the volume of the water displaced must be equal to the volume of the object. Furthermore, by Archimedes' Principle, upon immersion the object would receive a buoyant force equal to the weight of the water displaced. Thus, an object weighed in air and then weighed while immersed in water would have an effective weight that was reduced by the weight of the water displaced, if the buoyant force of the air is negligible. When weighed in air, the object receives a buoyant force equal to the weight of the air displaced by the object. However, the density of air is small enough (compared to the density of most solids) to allow this buoyant force to be neglected when weighing most solids in air. (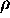_air = 1.3 x 10^-3 grams/cm³)

For an object more dense than water

SG = (W_S / V) / (W_W / V) = W_S / W_W = W_S / (buoyant force) = W_S / (loss of weight in water)
= W_S / (W_S - weight of substance in water)

This suggests a method for determining the SG of an object more dense than water; namely, weight an object in air and weigh it while completely immersed in water. The SG would then be the weight in air divided by the apparent loss of weight when weighed in water.

A device called a Jolly Balance is designed to measure the weight of objects in air and in water by reading the elongation of a spring. It utilizes a Vernier scale to read the elongation of the spring to the nearest 0.05 mm, and so is very precise. Hooke's law

F = - k x

should apply to the spring, where F is the force (weight) that stretches the spring by an amount x, and k is the spring constant. Substituting into the equation above, we find

SG = W_S / (W_S - weight of substance in water) = (k x_A) / (k x_A - k x_W)

When the unknown spring constant is canceled, the SG may be found using only the two spring elongations

x_A: the object in air
x_W: the object completely submerged in water

SG = x_A / ( x_A - x_W)

For an object less dense than water

The equation above is only true if the object is more dense than water. If the object is less dense than water, a lead weight must be attached and three spring elongations must be measured to determine the SG. The three elongations are

x_A: the object alone, in air
x_B: the object in air with the lead sinker submerged completed in water
x_C: both the object and the sinker completely submerged in water

The latter two elongations are used to determine the loss of weight in water, that is, the denominator of the SG definition. You should derive this formula in terms of x_A, x_B, and x_C.

SG = W_S / (loss of weight in water) = ?

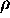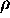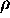Having determined the SG for sinking and floating objects using Archimedes' Principle and the Jolly Balance, it is desirable to use an independent method for comparison. Since SG = _S / _W, and since _W = 1 gram/cm³), one can determine the density of the object by measuring its mass and volume directly.

For a liquid

The Volumetric Flask (or Pycnometer) has a hollow stem stopper that allows one to prepare equal volumes of fluids very reproducibly. If the mass of the flask is measured (1) when empty, (2) when filled with the fluid, and (3)when filled with water, the SG of the fluid can be determined. Since the volume is the same, it will cancel out of the SG fraction.

Procedure

We will perform three separate experiments in which we will determine the density and specific gravity of

a solid more dense than water
a solid less dense than water
a liquid

Set up the Jolly Balance

Level the Jolly balance using the screws on the legs so that the scribed rod does not touch the clear plastic sleeve.
Set the Vernier scale to zero (0.00 cm) using the knob near the base.
Move the clear plastic sleeve until the scribe line on it is aligned with the scribe line on the hanging metal rod.
The Jolly balance is now calibrated to read zero when there is no load on the spring, so the clear plastic sleeve MUST NOT BE MOVED for the duration of the experiment.

Part 1- an object more dense than water

Measure the mass of the dense (dark colored) ball on a triple-beam balance.
Measure the diameter of the ball using a Vernier caliper several times. You decide how many. Choose many different orientations, not all in the same plane. (Why?)
Place the ball on the spring of the Jolly balance.
Turn the knob at the base until the scribe line on the metal rod is aligned with the scribe line on the plastic sleeve.
Record the spring elongation x_A.
Fill the large metal beaker with water to about 3/4 capacity and place it on the support table.
Next, the ball should be completely submerged and the scribe line on the metal rod should be aligned with the scribe line on the plastic sleeve. To achieve this, adjust the spring elongation using the knob at the base of the Jolly balance, and adjust the height of the support table, or adjust the level of water in the large beaker by filling it from the small beaker.
Record the spring elongation x_W.

Part 2 - an object less dense than water

Measure the mass of the floating (light colored) ball on a triple-beam balance.
Measure the diameter of the ball using a Vernier caliper several times. You decide how many. Choose many different orientations, not all in the same plane. (Why?)
Place the ball on the spring of the Jolly balance.
Turn the knob at the base until the scribe line on the metal rod is aligned with the scribe line on the plastic sleeve.
Record the spring elongation x_A.
Attach the lead sinker to the bottom of the floating ball.
Immerse all of the lead sinker, but none of the floating ball.
Record the spring elongation x_B.
Immerse both the lead sinker and the floating ball.
Record the spring elongation x_C.

Part 3 - a liquid

Measure the mass of the clean, dry pycnometer.
Fill the pycnometer to the top with alcohol from the "clean" bottle using a squeeze-bulb pipette. Be certain to use the pipette marked "ALCOHOL" to avoid cross contamination.
Insert the hollow stem stopper. Notice that some fluid will be forced out through the hollow stem. The volume of fluid in the pycnometer is now very reproducible; the pycnometer can be filled to the same level (namely the top of the hollow stem) with great precision.
Dry any alcohol that may have spilled on the outside of the pycnometer.
Measure the mass of the pycnometer filled with alcohol.
Spill the used alcohol into the "waste" bottle.
Rinse the pycnometer with water several times and fill it to the top using the pipette marked "WATER".
Insert the hollow stem stopper. Notice that some fluid will be forced out through the hollow stem.
Dry any water that may have spilled on the outside of the pycnometer.
Measure the mass of the pycnometer filled with water.
Spill the water into the sink and invert the pycnometer to dry.
For pure isopropyl alcohol, SG = 0.810, but if this is cut with 30% water then SG = 0.867. The latter should be used as the theoretical value for comparison.

Error analysis

Determine the SG of the dense ball using the Jolly balance measurements with an error estimate.
Determine the SG of the dense ball using the mass and volume measurements with an error estimate.
Compare the SG obtained by the two methods. Are they compatible?
Determine the SG of the floating ball using the Jolly balance measurements with an error estimate.
Determine the SG of the floating ball using the mass and volume measurements with an error estimate.
Compare the SG obtained by the two methods. Are they compatible?
Determine the SG of 70% isopropyl alcohol with an error estimate and compare with the theoretical value. Is the theoretical value within your error bars?
Identify at least two sources of statistical error.
Identify at least two sources of systematic error.
The air is a fluid in which you and the experiment are immersed. What is the fractional error incurred by neglecting the buoyant force of the air on each of the wooden spheres? That is, what is the mass of the displaced air divided by the mass you measured on the triple-beam balance? Justify the neglect of this buoyant force.

Back to the Mechanics Manual