Error Analysis
Name:_______________________________
4-digit Code Number:_______________________________
Partner(s):
Station number:
Error in this context does not mean mistake but rather refers to the
uncertainty in a measurement. All measurements in practice and even
in principle have some error associated with them; no measured quantity
can be determined with infinite precision.
Statistical Errors (also known as Random Errors)
Most measurements involve reading a scale. The fineness of the scale markings
(how close together they are) is limited and the width of the scale lines is
nonzero. In every case, the final reading must be estimated and is therefore
uncertain. This kind of scale-reading error is random since we expect that
half of the time the estimate will be too small, and the other half of the
time the estimate will be too large. We expect that random errors should
cancel on average, that is, many measurements of the same quantity should
produce a more reliable estimate. Statistical errors can be controlled by
performing a sufficiently large number of measurements.
The error estimate on a single scale reading can be taken as half of the
scale width. For example, if you were measuring length with a scale marked
in millimeters, you might quote the reading as 17.0 mm ± 0.5 mm.
If you measured the same length many times, you would expect the error on
the measurement to decrease. This is indeed the case.
The best estimate of the measured quantity is the mean or average of all the
measurements. Simply add all the individual measurements together and
divide by the number of measurements.
The best estimate of the error associated with the mean value is called the
"error on the mean" and is given by (the error on a single measurement)
divided by (the square root of the number of measurements). Obviously,
this will decrease as the number of measurements increases.
The final reading for a quantity should be quoted as:
(mean) ± (error on the mean).
Error Propagation
Addition and Subtraction
If several quantities with associated random errors are given by:
x ± 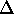 x, y ±
x, y ± 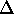 y, ... , z ±
y, ... , z ± 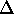 z, then
the sum or difference is given by q ±
z, then
the sum or difference is given by q ± 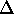 q where q might be
q where q might be
q = x + y - z
and the error on q is propagated from the errors on x, y, ... , and z
as follows
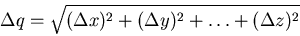
Notice that the errors are added in quadrature, even when the quantities
are being subtracted. The error always increases when adding or subtracting
quantities.
Multiplication and Division
If several quantities with associated random errors are given by:
x ± 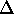 x, y ±
x, y ± 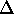 y, ... , z ±
y, ... , z ± 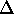 z, then
the product or quotient is given by q ±
z, then
the product or quotient is given by q ±  q where q might be
q where q might be
q = x*y/z
and the error on q is propagated from the errors on x, y, ... ,
and z as follows
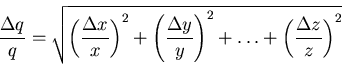
Systematic Errors
These errors are more insidious than statistical errors. Systematic errors
are difficult to detect, and the sizes of systematic errors are difficult
to estimate. Increasing the number of measurements has no effect on
systematic errors because the error is always in the same direction (all
measurements too high, or all measurements too low). Careful instrument
calibration and understanding of the measurement being made are part of
prevention.
For example, suppose that you are using a stopwatch to time runners in the
100-meter dash. You are quite adept at making the measurement, but
-- unknown to you -- the watch runs 5% fast. All times will be 5% too
high. There will be no immediately obvious indication of a problem.
If you happen to be familiar with the runners' normal times, you might
notice that everyone seems to be having a slow day. To prevent such
problems, one should calibrate the stopwatch with a known standard
such as the Nation Institute of Standards and Technology's standard
time service on short wave radio.
The rules are: 1) the error should have one significant figure; 2) the
number of decimal places in the measurement should be the same as the
number of decimal places in the error.
Always remember: There is no such thing as "human error". Try to find the
deeper cause for any uncertainty or variation.
Abstract
Data
Measure the length of your instructor's pencil. Remember the units and
an error estimate.
Table of measurements by the whole class
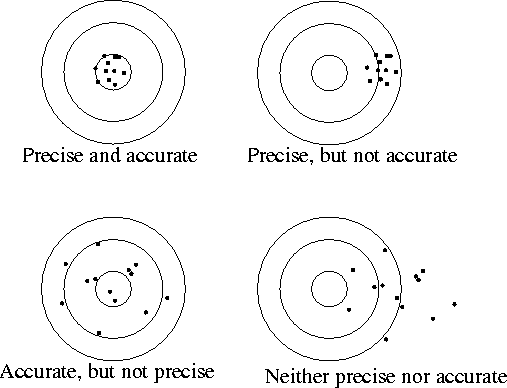
Make a histogram of the data.

Do you observe statistical (random) errors in the data plotted on the
histogram? Explain.
Do you observe systematic errors in the data plotted on the histogram?
Explain.
Identify several sources of error and label them as random or systematic.
What is the mean length of the pencil? (Use correct data only.)
What is the error on the mean length of the pencil?
Quote your answer as xbest ±  x
x
Compare the error on the mean length with the error estimate from the
measuring device.
Measure the length of a paper rectangle
Measure the width of a paper rectangle
Best estimate for the area
Smallest possible area
Largest possible area
There are two methods for computing the error on a quantity that you calculate
(as opposed to a quantity that you measure directly).
- Error on the area from (largest - smallest)/2 calculations
- Propagated error on the area from the formula
Quote your answer as Abest ±  A
A
What is the thickness of one page of any text book? Explain your
procedure and reasoning in detail so that another student can duplicate
your procedure. Remember to include units and an error estimate.
You should find that the error on the thickness is much less than the
thickness itself. In general, the error can be larger than the
measurement -- for example (0 ± 5) meters is perfectly acceptable,
but for this particular measurement the error should be smaller.
Conclusion
Summarize what you have learned today
(not what you have done).
 Back to the Mechanics Manual
Back to the Mechanics Manual
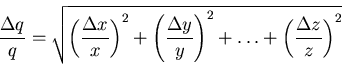


x
 Back to the Mechanics Manual
Back to the Mechanics Manual