Newton's First and Third Laws

Background

Read the sections of your lecture textbook dealing with Forces, Free-body Diagrams, and Newton's Second and Third Laws.

Rules for Drawing Free-body Diagrams

• Draw each object in isolation, that is, floating in space with no other objects in the picture.
• Attach only forces which act on the object, not forces which the object under consideration applies to other objects.
• The weight force always points down (toward the center of the Earth) and always has magnitude mg.
• The normal force can only push, not pull, perpendicular to the surface.
• The string tension force can only pull along the direction of the string.
• The friction force acts parallel to the surface, in a direction opposite to the velocity vector of the object.
• Forces act on one object and are caused by one object.
• An object can not exert a force on itself.
• Action-reaction partner forces never act on the same object.
• Action-reaction partner forces always have the same cause, that is, if one is gravitational then the other is gravitational; if one is normal then the other is normal.

Procedure

• Add a 200-gram load to the cart and measure the total mass using a triple beam balance at the instructor's desk. Include units and an error estimate.
• Multiply the mass of the loaded cart by g to calculate its weight. (g = 9.80 m/s² ± 0.01 m/s²)
• Set the angle of the incline to 15^o. The bottom of the indicator should be aligned to the angle mark.
• Tie a cord to the cart, pass the cord over the pulley, and attach a weight hook to the cord.
• The pulley should be extended as far as possible along its rod so that at the largest angles the vertical string is able to clear the lab bench.
• Adjust the pulley to make the cord parallel to the slope. (Why?)
• Add sufficient slot masses to the hook to achieve a rough equilibrium. It is not necessary to record this rough mass.
• Using slot masses as small as 1 gram, adjust the hanging mass so that the cart will move up the slope at a very slow constant speed (zero acceleration). For the error in the mass on the hanger, estimate how much mass must be added or subtracted to the hanger before you notice a difference in the behavior of the cart.
• Record the slope angle and the amount of hanging mass. Note that the hook itself has a mass of 50 grams.
• Readjust the hanging mass so that the cart will move down the slope at a very slow constant speed (zero acceleration). Record this new hanging mass.
• Calculate the average hanging mass from the up and down trials.
• Find the average tension in the cord at this angle from the average mass (upward and downward motion).
• Repeat for slope angles 20^o, 25^o, ... , 45^o (or as large as feasible).
• It is possible that at the lowest angle 15^o, the empty hanger itself may be too heavy to allow the cart to move down the ramp at constant speed. If this is the case, omit the data point at 15^o.

Error analysis

• Why is it necessary that the cord be parallel to the slope?
• Why is it necessary to roll the cart at constant speed?
• Why is it necessary to roll the cart both up and down the slope?
• Draw a free-body diagram for the cart. Determine from theory the tension required to achieve equilibrium as a function of angle.
• Plot the measured average string tension T (vertical axis) vs. the angle of inclination 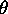(horizontal axis). Compare this to the curve predicted from theory. The data should appear as points; the theory should be a solid curve. Do not fit the data points by eye; do not draw the best straight line though the data (they do not lie on a straight line). Simply plot the data and theory on the same set of axes and observe how closely they match.
• Calculate the propagated error on the tension for each angle. Are the error bars on your plotted data points visible on this graph, or are they too small to be seen?
• The first student to email me (Dr. Scalise) with the correct answer to the following question will receive 10 points added to their final exam grade. What is the sum of the prime numbers between 1 and 110? It pays to read the labs carefully in advance. (Do not email. This question has already been answered for Fall 2010. The answer was sent on 24 September 2010.)
• Identify at least two sources of statistical error.
• Identify at least two sources of systematic error.

Back to the Mechanics Manual