Linear Momentum
Procedure
- Carefully unscrew the hinge pin of the pendulum.
- Measure the mass of the one ball which you will use throughout this
experiment, and separately measure the mass of the
(ball plus the pendulum without
the hinge pin), using the triple
beam balance at the instructor's desk.
- Carefully reattach the pendulum to the base with the
hinge pin.
- Level the ballistic pendulum using the built-in bubble level. Adjust the
height of the legs by turning the feet.
- Use the C-clamp to attach the gun base rigidly to the lab bench. This
will prevent recoil of the gun. Ensure that the base is still level
even after the C-clamp is attached.
- Measure the length of the pendulum from the center of the hinge pin to
the center of mass of the pendulum, labeled C/M on the pendulum shaft.
- Place the metal ball whose mass you recorded on the end of the gun,
and push back until the spring locks into position.
- Make sure that the pendulum is hanging freely, but is not swinging.
Do not change the spring tension using the knob at
the end of the gun during the experiment. Fire the gun.
- After the pendulum comes to rest, read the angle to which the
pendulum has risen. If the red indicator falls on a black line, the
number of degrees is even; if the red indicator falls between
adjacent black lines, the number of degrees is odd.
- Repeat the last three steps several times.
Error analysis
- Use the prelab assignment to derive a formula for the muzzle velocity
vm using only the following five variables
- the small projectile mass, m
- the larger (ball+pendulum) mass, M
- the length of the pendulum, L
- the angle to which the pendulum rises,
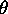
- the acceleration due to gravity,
g = 9.80 m/s2 ± 0.01 m/s2
- Calculate the average muzzle velocity with an error estimate.
Take the error in the angle to be zero.
You will not be able to propagate the error in the muzzle velocity
until you have a formula with vm on one side of the equals
sign and the five measured quantities on the other side.
- How does this speed compare to the muzzle velocity measured in the
Acceleration and Freefall Lab?
Which result is more reliable and why?
- Why is it incorrect to equate the kinetic energy lost by the
projectile to the potential energy gained by the projectile/pendulum
combination? In other words, why is mechanical energy not conserved
in this experiment? Where does it go?
- Calculate the kinetic energy of the bullet before the collision. No
error estimate is required.
- Calculate the change in potential energy of the bullet and pendulum after
they have both come to rest.
No error estimate is required.
- Identify at least two sources of statistical error.
- Identify at least two sources of systematic error.
 Back to the Mechanics Manual
Back to the Mechanics Manual
 Back to the Mechanics Manual
Back to the Mechanics Manual