Refraction - Big Picture

Refraction is the bending of rays of electromagnetic radiation (like visible light, radio waves, ultraviolet rays, etc. ) at an interface between different materials due to differences in the propagation speed of the radiation through the materials.

The speed of light (short for all forms of electromagnetic radiation) in a material is slower than the speed of light in vacuum c=299,792,458 meters/second by a numerical factor called the index of refraction n, where n=1 for vacuum and n>1 for materials. For example, the index of refraction of air is about n_air~1.000277 depending on air temperature, density, and so forth. The index of refraction of water is about n_water~1.33, again depending on temperature, impurities, etc. The speed of light in water is thus

v_water = c/n_water = (299,792,458 m/s) / 1.33 = 225,407,863 m/s.

Since the speed of light is water is less than the speed of light in air, there will be refraction or bending of the path of light rays at an air/water interface.

The reason that you can tell there is a glass sphere in someone's hand, even though the glass is perfectly clear, is that the index of glass (1.33) is different from the index of air and your brain recognizes the bending of light rays as caused by a clear object.

If you immerse the glass spheres in a medium like water with an index close to glass (1.33), then the glass spheres will disappear. The indices of refraction on both sides of the glass/water interface are similar, so the light ray are not bent.

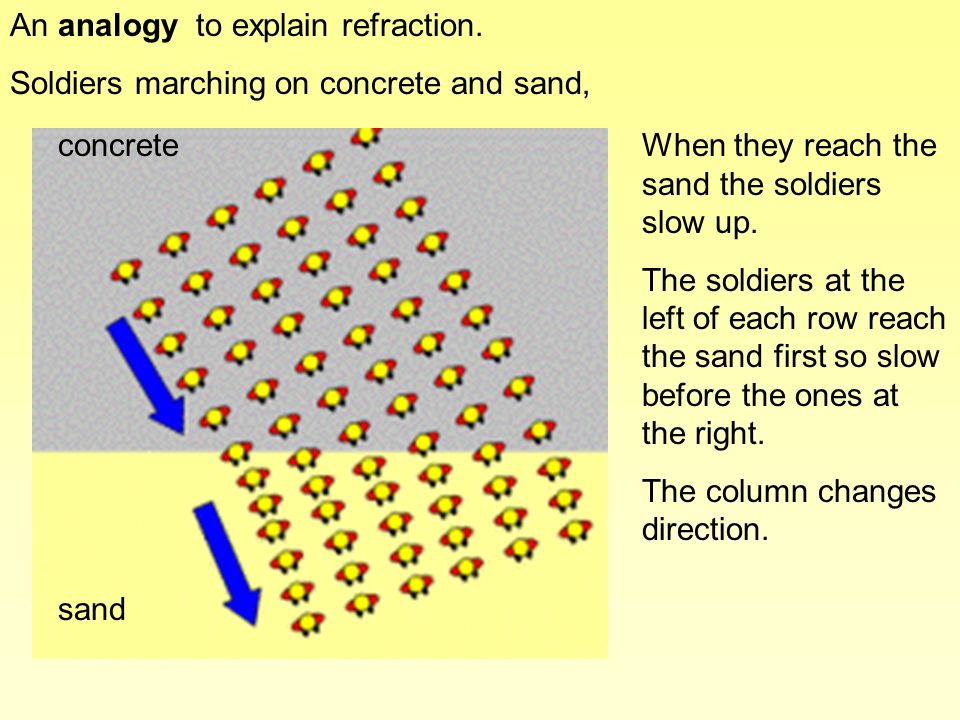
A very good analogy to understand the refraction or bending of a light ray is a marching column that moves from one medium (say concrete) on which the marchers can move quickly, to another medium (say sand) on which they must move more slowly. The rows of marchers are like the wavefronts of a plane electromagnetic wave. The diagram below shows how the direction in which the parade moves changes simply because the individual marchers are slowing down as they enter the new material.

Snell's Law

The amount of bending of light rays toward or away from the normal direction (the dashed lines perpendicular to the interfaces in the figure below) is given by Snell's law.

n₁ sin(θ₁) = n₂ sin(θ₂)

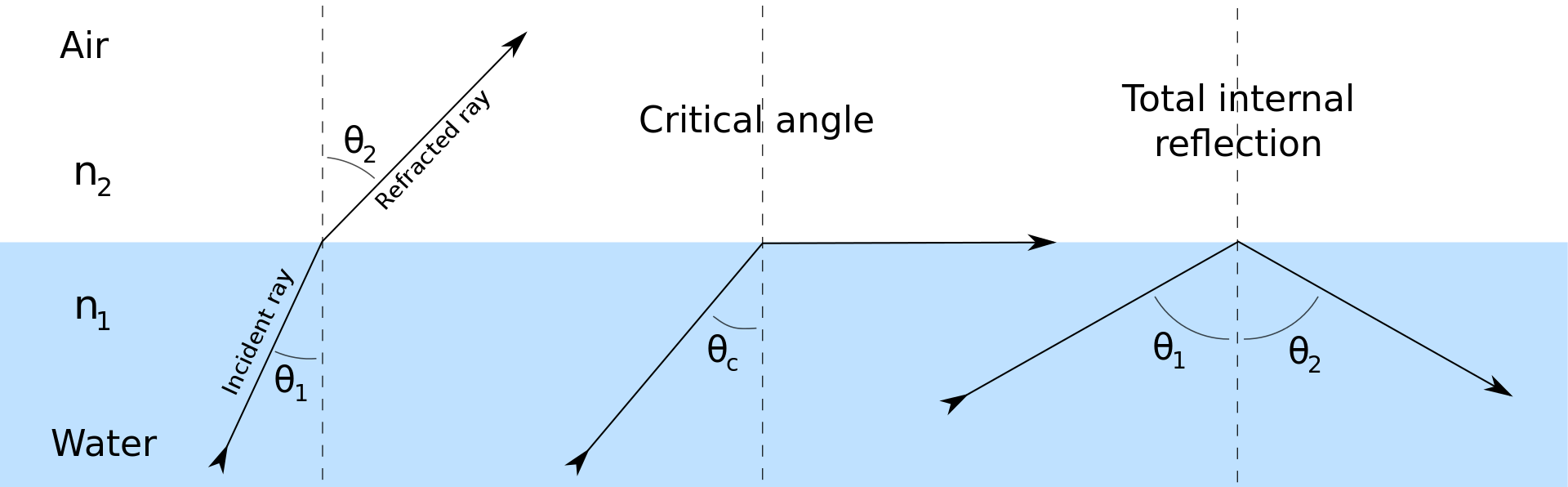
When the angle in the material with the smaller index of refraction exceeds 90 degrees, none of the light is refracted and instead all of the light undergoes total internal reflection. This is the principle which allows fiber optic cables to carry light signals around curves in the cable.

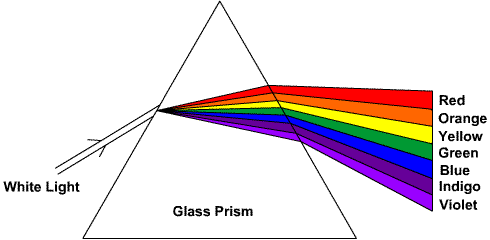
Dispersion is the spreading of different frequencies of light due to the fact that the speed of light in a medium depends on the frequency. For example, in a glass prism, red light travels faster than violet light. Alternatively, the refractive index n_red < n_violet. Notice in the diagram below that the violet ray is bent through a sharper angle than the red ray. In vacuum, of course, all the frequencies travel at the same speed c and there is no dispersion.

SPECIFIC OBJECTIVES

To become familiar with the use of a spectrometer; to understand how the index of refraction varies with the wavelength of light.

EQUIPMENT

Spectrometer, glass prism, mercury light source, high-voltage power supply.

BACKGROUND

A spectrometer is designed to measure the angle between two beams of light. One beam goes straight through the spectrometer and the other beam is deviated by some device such as a glass prism or a diffraction grating. The angle between these two beams is called the angle of deviation (D). A spectrometer consists of the following parts:

light source
collimator and slit
table
telescope
angle scale

The light source must involve whatever material is being investigated and that material must be excited to produce (visible, in this case) electromagnetic radiation (light). A frequently used source consists of a sample of the substance to be investigated kept at a very low pressure in a capillary tube. When this tube is provided with a high enough voltage across its ends, a current will flow through the tube. The current electrons will interact with the atomic orbital electrons and the latter will gain energy. When the orbital electrons release this excess energy, it is in the form of electromagnetic radiation which may or may not be visible. What startled early spectroscopists was that the emitted radiation consisted not of every color, but of discrete wavelengths (

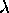) and every chemical element had a unique set of wavelengths (called the spectrum of the element) which could be used to identify that element with certainty.

The collimator is simply a tube of adjustable length which is used to make the light rays from the source parallel. On the end of the collimator, facing the source, is a variable width slit which is used to allow more or less light into the spectrometer.

The prism (this lab) or diffraction grating (next lab) is mounted on the table which can be rotated to adjust the angle of incidence of the beam from the collimator.

Within the telescope is a hairline which facilitates centering the telescope on the image of the slit. Both the slit and the hairline must be well focused to accomplish this. The telescope is mounted in such a way that it can be rotated about a central, vertical axis.

Attached to the telescope is an angle scale which allows the angle through which the telescope rotates to be directly measured. The angle scale is calibrated to read 0.0^o when the hairline is centered on the straight through beam. There is a vernier scale to provide reading precision to the nearest tenth of a degree (0.1^o).

If the angle of incidence of the light beam on the prism is changed by rotating the table on which the prism sits, the image of the slit will move toward 0.0^o. If the table is rotated further, the image of the slit will stop for an instant then begin to move away from 0.0^o. Thus, the angle of deviation has passed through a minimum value, D_m.

The formula relating the angle of minimum deviation of a particular wavelength to the index of refraction (n) for that wavelength is

n = sin[(A+D_m)/2] / sin(A/2) where "A" is the apex angle of the prism.

PROCEDURE

Calibrating the Spectrometer

Place the power supply on the base (2-kg mass) so that the narrow, bright part of the light source capillary tube is aligned with the collimator. Turn on the power supply.
Open the slit on the end of the collimator by turning the silver knob. Look through the telescope while moving it back and forth until you find the illuminated slit. Focus the slit by moving the barrel of the telescope in and out. Focus the hairline by moving the eyepiece in and out. Rotate the slit until it is vertical. Rotate the eyepiece until the hairline is vertical. You may need to move the light source (carefully!) so that the slit is maximally bright.
Open and close the slit while looking through the telescope. Notice that only one side the slit moves; the other side is stationary. Place the hairline over the side of the slit that does not move, on the boundary between light and dark.
While keeping the hairline on the stationary side of the slit, rotate the angle scale until it reads 0.0^o. Lock the angle scale by turning the silver knob at the base of the spectroscope. The scope is now calibrated; from now on the angle scale will move with the telescope as it is rotated. Do not loosen the screw at the base of the scope at any point during the lab.

Measuring the Apex Angle (A)

Open the slit to its maximum width. Check to see that the slit is vertical, well-focused, and at its maximum brightness.
Handle the prism extremely carefully! It is very expensive and very fragile.
Rotate the table until the post is in front of the telescope. Place the prism on the table with the apex angle (A) facing the source, and with the apex near the center of the table. The frosted side of the prism opposite the apex angle should touch the post. Clamp the prism in place. The prism must be located such that the wide beam from the fully opened slit is split by the apex. Each part of the beam will be reflected from the two sides of the prism. The law of reflection may be applied to show that the total angle between these two reflected beams is 2A.
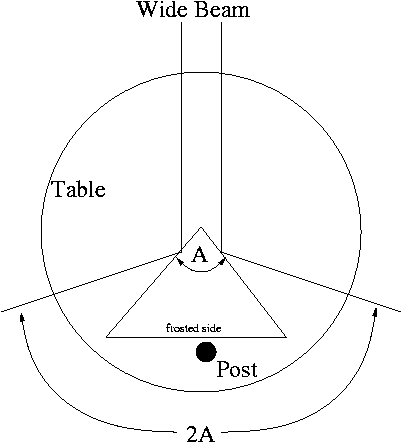
By eye, adjust the prism so that the frosted side is perpendicular to the beam and the apex is in the middle of the beam. Place the black cloth over the table.
Swing the telescope to both sides of zero and locate both beams. Do not take any angle measurements until both beams are visible. If neither reflected beam appears, it may be because the light source is not directly in front of the slit. Try moving the source slightly from side to side. If one beam appears, but the other does not, the reason may be that the prism is misaligned and all the beam from the source is reflecting from one side of the prism, while none is reflecting from the other side of the prism. Remove the cloth and rotate the table slightly to place the apex in the center of the beam. Lock the table in place using the set screw under the table. Replace the black cloth.
Once the reflected beams are visible on both sides of zero, measure the angles on both sides by aligning the hairline with the side of the slit that does not move. But remember, this is a reflection so left and right will be reversed. Measure each angle to the nearest tenth of a degree.
Average the two angles away from zero to find the apex angle (A) of the prism. It will be necessary first to subtract one angle from 360^o.

Minimizing the Angle of Deviation

Remove the black cloth, loosen the table set screw, and rotate the table so that the frosted side of the prism and the post are near 10 o'clock (with the source at 12 o'clock). One of the clear sides of the prism should be perpendicular to the beam from the source, and the apex should be near the center of the table. Replace the black cloth.
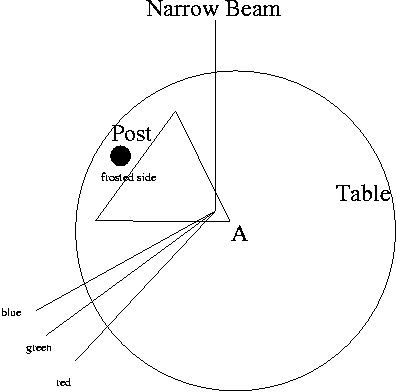
Move the telescope to the left of zero and find the refracted beams.
Once you locate the mercury spectrum, narrow the slit until it is just a few times wider than the hairline. You may need to reposition the light source so that the slit is maximally bright.
Reach under the black cloth and rotate the table. The spectral lines will shift to the right, stop, and shift to the left. Find the table position which puts the lines at their rightmost extent and lock the table in place. The angle of deviation has been minimized. Do not touch the table or the prism for the remainder of the experiment.

Measuring the Angle of Minimum Deviation (D_m)

Move the telescope until the hairline is aligned with the stationary side of the narrow slit (this is NOT a reflection) for each color. Record the angle away from zero to the nearest tenth a degree for each color listed in the table below. Repeat your measurements more than once and average.

Wavelength (Angstroms)	Color	Intensity
5790.66	Yellow	Strong
5769.60	Yellow	Strong
5460.74	Green	Strong
4916.07	Blue-Green	Weak
4358.33	Violet	Stronger
4077.83	Violet	Weak
4046.56	Violet	Less Strong

The yellow lines form a doublet, a pair of lines very close together. If you can only distinguish one yellow line, narrow the slit and make sure that it is in sharp focus. The separation between the two yellow lines will be roughly the width of the hairline.
The two yellow lines, the green line, and the stronger violet line are easily visible with the room lights on. Viewing the other lines may require complete darkness. It often helps to look slightly to one side of the line because the rod photoreceptor cells in your eyes are more numerous away from center. Below is a sketch of the relative line locations, separations, and intensities.
When the room is dark to accommodate seeing the faint spectral lines, it is difficult to see the hairline. This can be illuminated periodically with the flashlight.
There should not be any red in the mercury spectrum. If colors other than the ones listed in the table are visible, they are due to the presence of singly ionized mercury, Hg II, or an impurity such as nitrogen gas from the atmosphere leaking into the tube.
Some spectrum tubes may give two blue-green lines. If this is the case, measure the one closer to the violet side of the spectrum. The spurious line is due to the presence of singly ionized mercury, Hg II.

Analysis

Use D_m for each color to calculate n for each color. The error in n and the number of significant figures in n are determined by finding the largest and smallest n's consistent with your measured D_m. That is, D_m can range from a low value of (D_m - its error) to a high value of (D_m + its error). Each end of this range corresponds to a different n.
Plot n (vertical axis) vs. 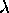(horizontal axis) for the seven visible mercury lines.
Fit the best function through your data points. It is not expected that the curve will be any particular function; you will merely determine an empirical relationship between the index of refraction and the wavelength. DO NOT FIT A STRAIGHT LINE THROUGH THE DATA POINTS. It will be obvious from your plot that the data are not linear.
The prism manufacturer asserts that the prism has n=1.65 for some particular wavelength (not necessarily one of the seven mercury wavelengths).
1. What should be the angle of minimum deviation for this wavelength?
2. Use your plot to determine the corresponding wavelength and color.
Identify two sources of random error and two sources of systematic error.

Back to the Electricity and Magnetism Manual

References

Halliday, Resnick, & Walker, Fundamentals of Physics Vol. 2 (10th ed.), Ch 33: Electromagnetic Waves, Wiley, 2014.
Hyperphysics (http://hyperphysics.phy-astr.gsu.edu/hbase/hph.html)