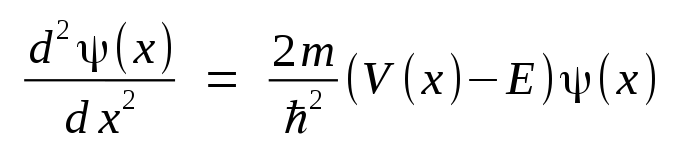
Whereas the wave packet application here constructs packets of waves that satisfy the Schrödinger equation corresponding to an unbound particle, a particle in a uniform region of potential, this application explores wave packets constructed so that they correspond to a particle bound in a potential well.
The bound energy levels application will solve the Schrödinger equation for a variety of potential well profiles and numerically search for the allowed energy levels that allow a normalizable wave function solution. Wave packets corresponding to a particle bound in these wells must be constructed only of the allowed wave eigenfunctions that are solved for each well profile, and not from any arbitrary distribution of wave momenta as in the unbound case.
When the time-independent Schrödinger equation
is solved for an energy bound level within potential well, only certain eigenfunctions ψj with their corresponding energy levels Ej will be allowed solutions that satisfy the boundary conditions of the well. But any linear combination of these allowed eigenfunctions

will also be solutions of the Schrödinger equation, where the cj are arbitrary linear combination coefficients. Then the full solution including time dependence will be of the form
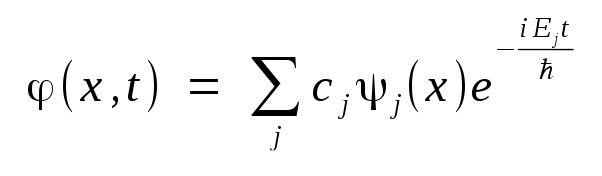
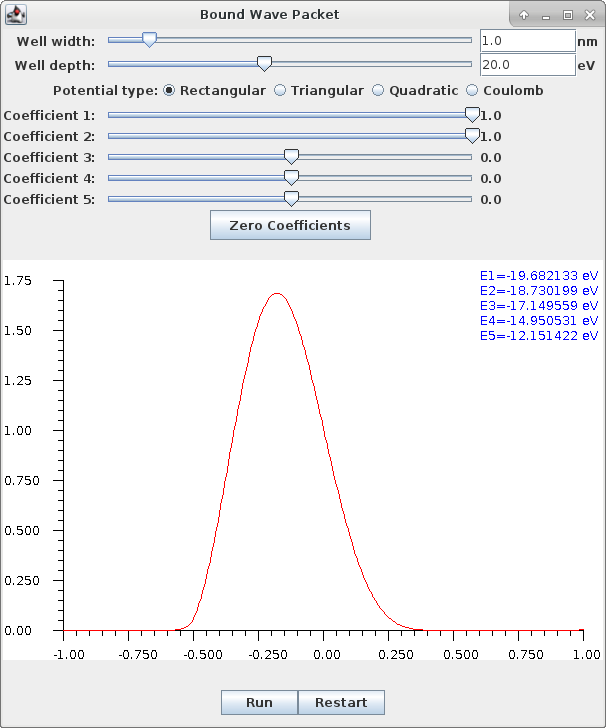
This application will accept the same specification of well profiles and dimensions as in the bound energy levels application, and solves for the lowest five allowed energies a bound electron may assume in various energy states, together with the corresponding wave eigenfunctions. It then allows the user to to construct a wave packet interactively by specifying up to five coefficients with which to form a linear combination of the eigenfunctions. By a suitable combination of two or three wave functions, an initial wave function can be interactively constructed that shows a concentrated probability of the particle appearing toward one side of the potential well. Starting the time animation of the application then simulates the progression of the time dependent factor of the full wave function solution, and the oscillation of the electron back and forth in the well can be clearly observed.
For example, consider the probability distribution corresponding to a wave function composed of an equal linear combination of the two lowest energy eigenfunctions of an electron bound in a rectangular potential well, which looks like:
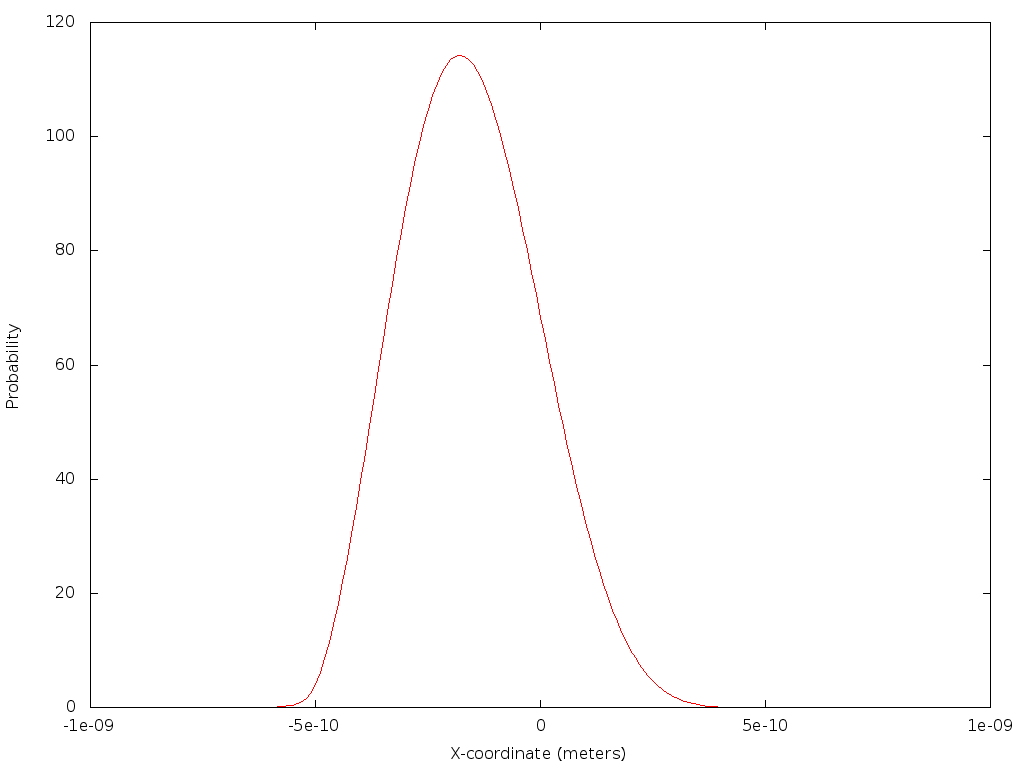
(Ignore the scaling on the vertical axis; to save computational time, the finalwave function summation plotted here has not been actually normalized.) Note that with the combination of two allowed wave functions, the probability distribution is now asymmetrically dominated with the electron being to the left of the center of the well. As the time dependence of the full Schrödinger equation solution evolves, the Java application will show this peak of probability distribution oscillate back and forth in the well.
Run from a shell or command terminal in the download directory with:
java -jar BoundWavePacket.jar
The default linear combination is an equal sum of the lowest two energy levels. Starting the animation shows a distinct and slow quantum particle oscillation. Try other eigenfunction combinations clustered around higher energies to see the oscillation frequency increase. Various profiles of the well potential can be chosen: Rectangular, Triangular, Coulomb and Quadratic. The quadratic profile corresponds to the quantum harmonic oscillator.
Back to Computational Physics Playground page
Back to John Fattaruso's home page