Diffraction Grating
SPECIFIC OBJECTIVES
To understand how a diffraction grating works; to understand the diffraction
grating equation.
EQUIPMENT
Spectrometer, diffraction grating, mercury light source,
high-voltage power supply.
BACKGROUND
A diffraction grating is made by making many parallel scratches on the
surface of a flat piece of transparent material. It is possible to put a
large number of scratches per centimeter on the material, e.g., the grating
to be used has 6,000 lines/cm on it. The scratches are opaque but the areas
between the scratches can transmit light. Thus, a diffraction grating becomes
a multitude of parallel slit sources when light falls upon it.
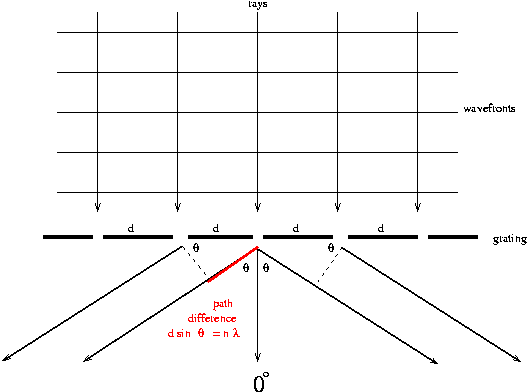
A parallel bundle of rays falls on the grating. Rays and wavefronts
form an orthogonal set so the wavefronts are perpendicular to the rays
and parallel to the grating as shown. Utilizing Huygens'
Principle, which is that every point on a wavefront acts like a
new source, each transparent slit becomes a new source so cylindrical
wavefronts spread out from each. These wavefronts interfere either
constructively or destructively depending on how the peaks and valleys
of the waves are related. If a peak falls on a valley consistently
(called destructive interference), then the waves cancel and no light
exists at that point. On the other hand, if peaks fall on peaks and
valleys fall on valleys consistently (called constructive
interference), then the light is made brighter at that point.
Consider two rays which emerge making an angle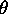 
with the straight through line.
Constructive interference (brightness) will occur if the difference in
their two path lengths is an integral multiple of their wavelength
(
) i.e., difference =
n
where n = 1, 2, 3, ... Now, a triangle is formed, as
indicated in the diagram, for which
n =
d sin( )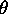
and this is known as the DIFFRACTION GRATING EQUATION. In this
formula 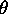is the angle
of emergence (called deviation, D, for the prism) at which a
wavelength will be bright, d is the distance between slits (note that
d = 1 / N if N, called the grating constant, is the number of lines
per unit length) and n is the "order number", a positive integer
(n = 1, 2, 3, ...) representing the repetition of the spectrum.
Thus, the colors present in the light from the source incident on the
grating would emerge each at a different angle
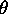since each has a different
wavelength .
Furthermore, a complete spectrum would be observed for n = 1 and
another complete spectrum for n = 2, etc., but at larger angles.
Also, the triangle formed by rays to the left of 0o is identical
to the triangle formed by rays to
the right of 0o but the angles
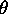R and
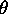L (Right and Left)
would be the same only if the grating is perpendicular to the incident beam.
This perpendicularity is inconvenient to achieve so, in practice,
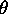R and
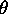L
are both measured and their average is used as
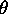in the grating equation.
PROCEDURE
Calibrating the Spectrometer
Read and follow the procedures
for calibrating the spectroscope found in the previous experiment.
The calibration can be performed with the grating in place on the table.
Measuring
- CAUTION: The diffraction grating is a photographic reproduction and
should NOT be touched. The deeper recess in the holder is intended
to protect it from damage. Therefore, the glass is on the shallow side of
the holder and the grating is on the deep side.
- Place the grating on the center of the table with its scratches running
vertically, and with the base material (glass) facing the light source.
In this way, one can study diffraction without the complication of
refraction (recall from the previous lab how light behaves when traveling
through glass at other than normal incidence). Fix the grating in place
using masking tape.
- Rotate the table to make the grating perpendicular to the incident beam
by eye. This is not critical since the average of 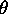R and 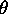L accommodates a minor misalignment.
- Affirm maximum brightness for the straight through beam by adjusting the
source-slit alignment. At this step, the slit should be narrow, perhaps a
few times wider than the hairline. Search for the spectrum by moving the
telescope to one side or the other. This spectrum should look much like that
observed with the prism except that the order of the colors as you move
away from zero degrees is reversed.
- Search for the second- and third-order spectra. Do not measure the
higher-order angles, but record the order of colors away from zero degrees.
- For each of the seven
colors in the mercury spectrum, measure the angles
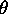R and
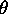L to the nearest
tenth of a degree by placing the hairline on the stationary side of the slit.
Analysis
- Average the right and left angles for each color.
- Use the grating equation with d=(1/6000) cm to find the wavelength
for each color.
Remember that 108 angstrom = 1 cm.
- Calculate the percent deviation for each wavelength using
% deviation = (data-theory)/theory x 100%
where "theory" is the tabulated wavelength from the last experiment.
Do not ignore the sign; it contains information. A positive % deviation
means that the value is above the theory; a negative % deviation
means that the value is below the theory.
- Do you notice any systematic problems in your seven % deviations?
- Use the grating equation with the
tabulated values of
from last time and your
measured values of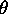
to calculate seven different values of N, the grating constant (N=1/d).
- Average the seven values of N. For the error on N, use the
standard deviation on the mean (SDOM). Compare your answer to the
accepted value of 6000 lines/cm. Does your value of N agree with the
manufacturer's value within the error range? See Taylor page 5
if you are confused.
- What could be causing any discrepancy?
- Why is it necessary that the base side of the grating face toward the
light source? Draw a ray diagram for the two cases: a) base toward the
source (correct) and b) grating toward the source (incorrect).
- A certain color emerges at 15o in the first-order spectrum.
At what angle would this same color emerge in the second order if the same
source and grating are used?
Don't forget your two random and two systematic error sources.
Back to the Electricity and Magnetism Manual