Forces in Equilibrium
Procedure
- Level the force table and put one of the
three pulleys at the angle 0o.
- Add 200 grams of mass to each of the three hangers, and remember
that the mass of the hanger itself is 50 grams.
- Arrange the other two pulleys such that the ring connecting the
different strings remains fixed at the center of the table (not
touching the central post). Tap the table gently to ensure that
the ring remains fixed. At this point, the ring is in equilibrium.
- Record the tension in each string T1, T2,
T3 and the angular
position of each pulley
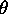 1,
1,
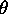 2,
2,
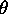 3.
3.
- Find the x and y components of each tension force. Take the
origin to be the central post, the positive x-axis to extend
through the 0o mark, and the positive y-axis to extend
through the 90o mark.
- Find the resultant force vector algebraically by adding the
respective components of the individual string tensions.
- Using the protractor provided, add the three tension force vectors
graphically by drawing arrows of an appropriate length in the
correct direction and connecting them tail-to-head. Try to use
an entire page of graph paper. Do not force
the triangle to close; experimental error might prevent this.
- Repeat the steps above for three masses not all the same
(e.g. 100 grams on hanger 1; 200 grams on hanger 2; and 300 grams on
hanger 3).
Error analysis
- Take the error in all the masses to be
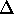 m = 1 gram.
m = 1 gram.
- Remember that g = 9.80 m/s2 ± 0.01 m/s2.
- Take the error in the angles measured on the force table to be
negligible.
- Find the errors in all the tension force components.
- Find the error in the resultant force x and y components using the
formula from the Error Analysis Lab:
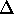 Fx
= [
(
Fx
= [
(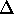 T1x)
2 +
(
T1x)
2 +
(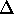 T2x)
2 +
(
T2x)
2 +
(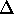 T3x)
2
]½
T3x)
2
]½
- In this experiment, we assume that the ring is massless.
If the central ring were to have considerable weight (comparable
to the string tensions), what new steps would be required in this
experiment? Assume that you can not add more mass to the hooks.
- Identify at least two sources of statistical error.
- Identify at least two sources of systematic error.
 Back to the Mechanics Manual
Back to the Mechanics Manual
 Back to the Mechanics Manual
Back to the Mechanics Manual